整理自 CMU 15-779 Lect 12，从数据并行到 ZeRO，解答了是如何把大模型塞进有限的显存里的问题。
Data Parallelism
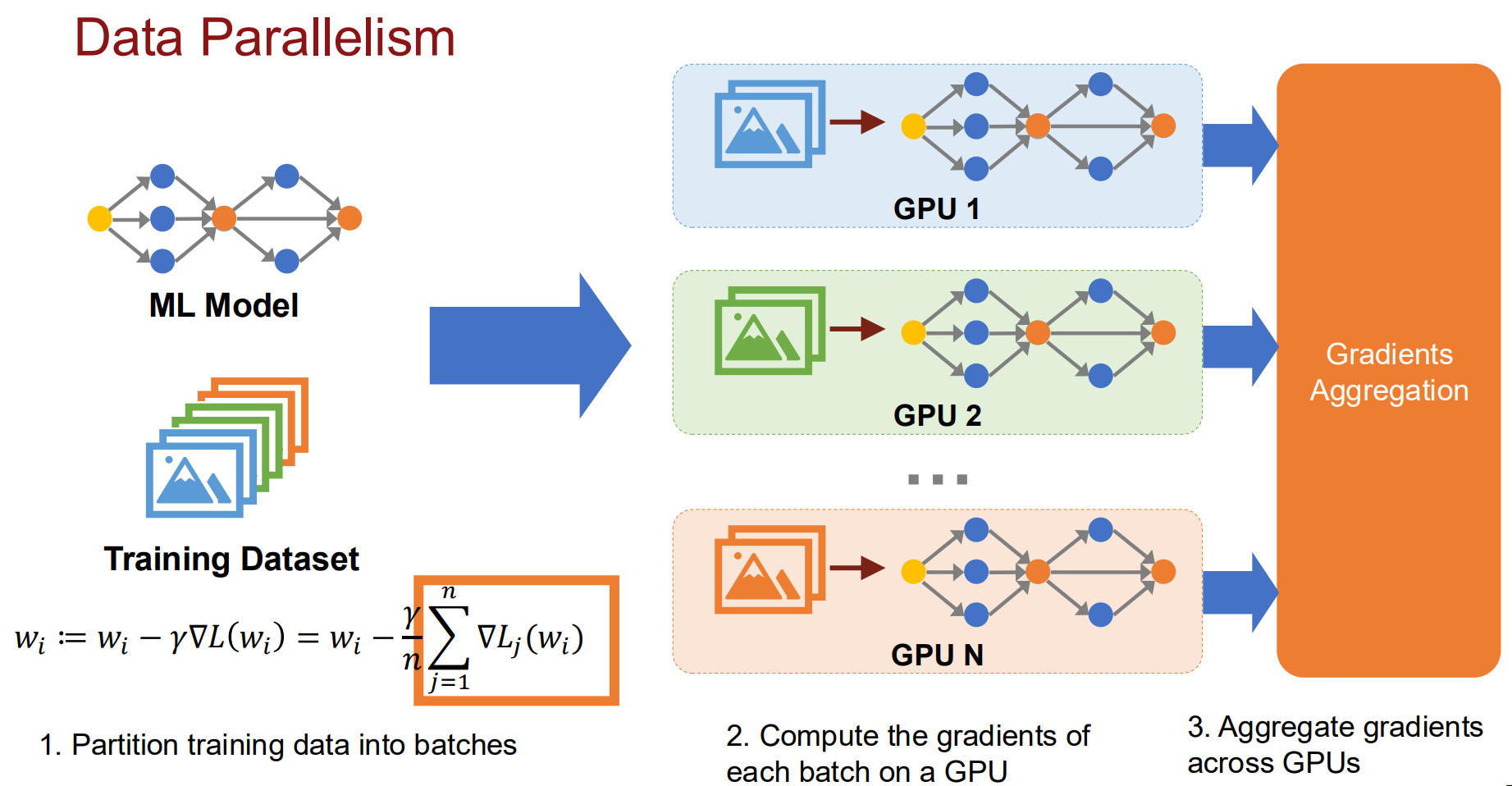
训练本质上是计算梯度并更新权重。数据并行直观理解就是如果有 $ N $ 个 GPU，那么把总的 Batch Size 分成 $ N $ 份。
在第 $ k $ 个 GPU上的计算过程：
- Local Gradient：基于本地数据 $ x^{(k)} $ 计算梯度 $$ g^{(k)} = \nabla L(w_t, x^{(k)}) $$
- All-Reduce：计算全局平均梯度 $$ \bar{g} = \frac{1}{N} \sum_{k=1}^{N} g^{(k)} $$
- Weight Update：所有 GPU 使用相同的 $ \bar{g} $ 更新权重 $$ w_{t+1} = w_t - \eta \cdot \text{Optimizer}(\bar{g}, \text{State}_t) $$ 这时每个 GPU 上都会有一样的完整模型副本，各算各的梯度，最后在汇总计算。
实现方法
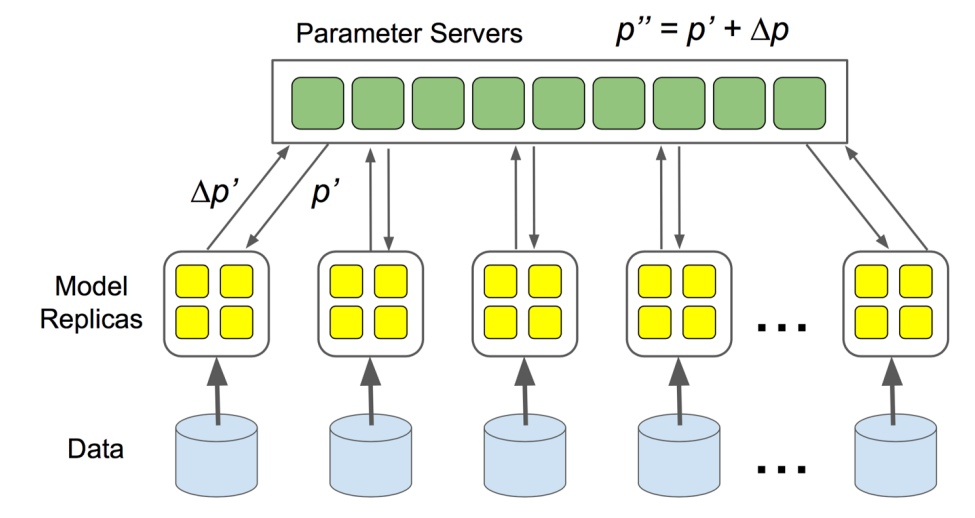
早期的实现方案是使用一个 Parameter Server，当 Server 接收到所有人的梯度以后再汇总更新。但是这样当 GPU 数量增多时，中心服务器的带宽就会出现不足，从而导致无法扩展。
这就引出了下面的核心问题，“如何去中心化？”。
All-Reduce
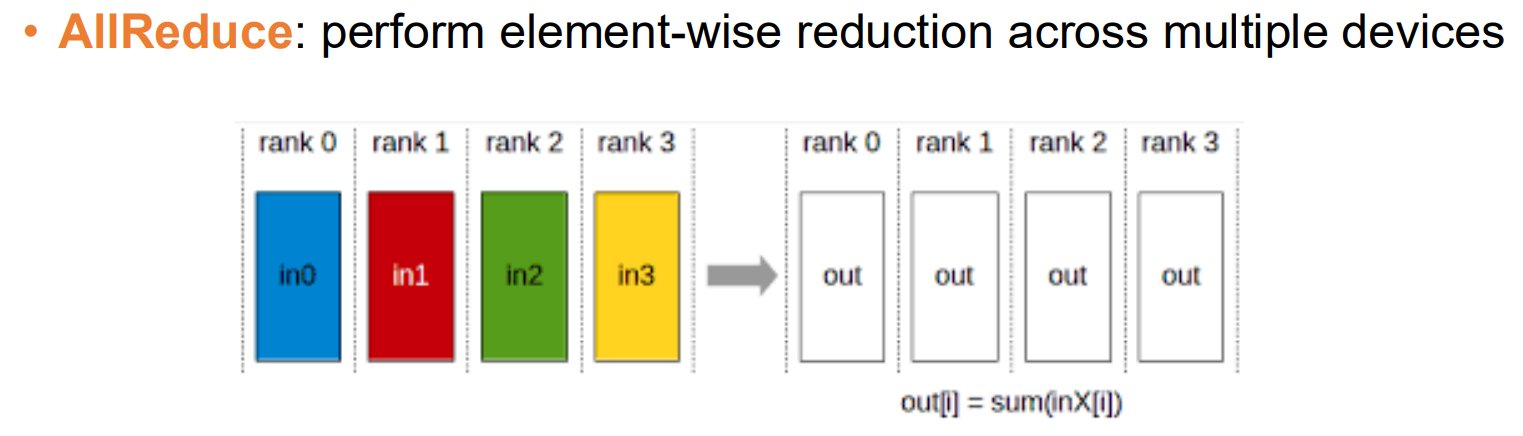
我们可以把上面的问题抽象为，如何让 $ N $ 个设备在没有一个“中心”的情况下，通过互相通信，最终每个设备都能得到数据的均值？这个过程在数学上被称为 AllReduce。 $$ \text{out}[i] = \sum \text{in}^{(k)}[i] $$ 一般除了 Naive 外一般有 Ring AllReduce, Tree AllReduce, Butterfly AllReduce 三种方法实现 AllReduce，其中 Ring AllReduce 最好，因此其余方法在此处略过。
Ring AllReduce
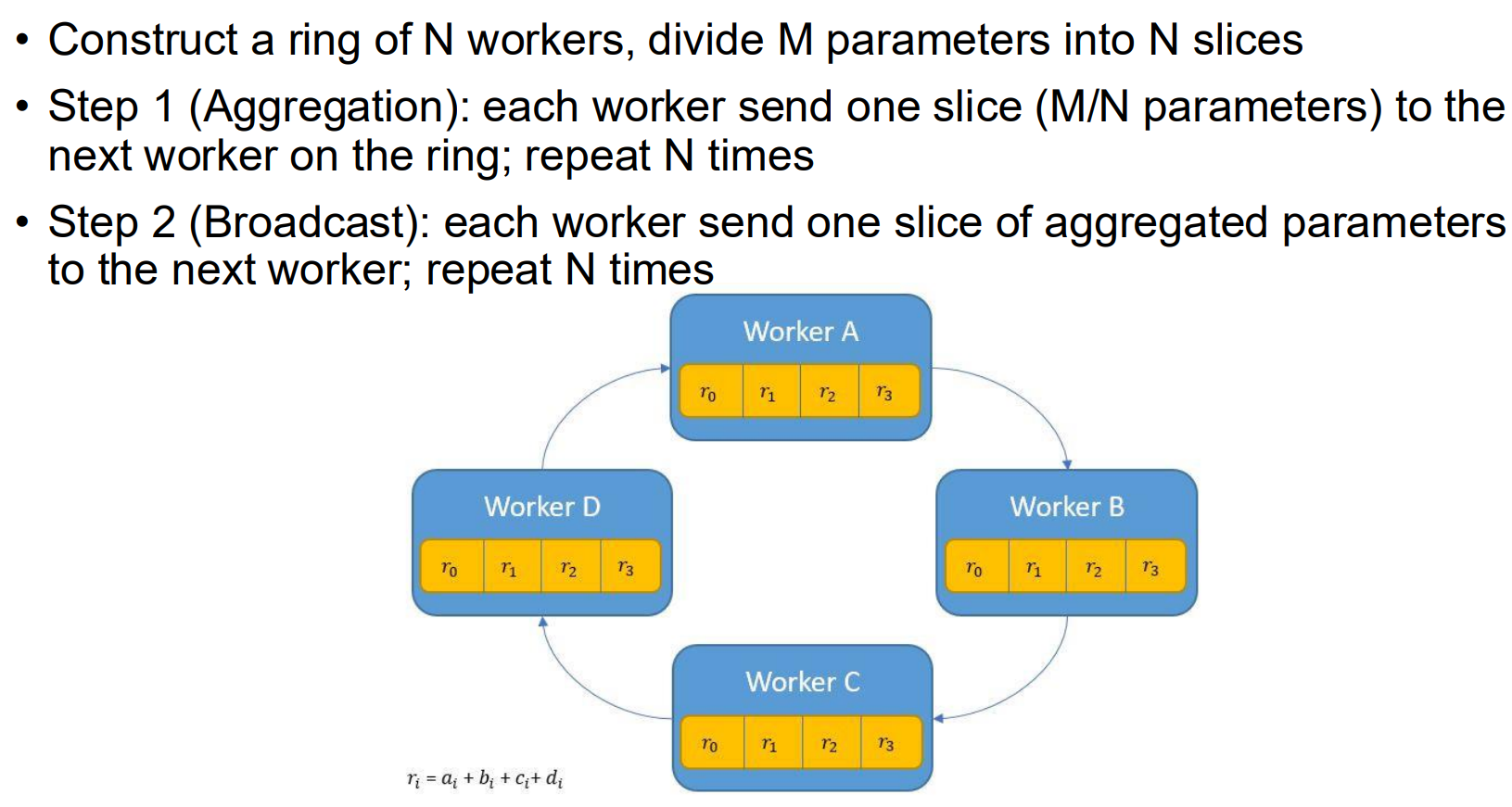分为 Scatter-Reduce 和 All-Gather 两个阶段。
Scatter-Reduce 阶段的目标是让每张 GPU 负责算出模型参数中某一块片段的总和。原理：假设参数量是 $ M $，有 $ N $ 张卡。我们将数据切成 $ N $ 块。在 $ N-1 $ 轮迭代中，每张卡同时发送自己的一块数据给邻居，并接收邻居传来的另一块数据进行累加。每一块数据在环里转了一圈，最终汇聚到了对应的 GPU 上。
All-Gather 阶段的目的是把第一轮的结果广播给所有人。每次迭代把算好的数据传递给下一个设备，并收到上一个设备的数据存下来。迭代 $ N-1 $ 轮后每个设备就都存有完整的数据了。
整个过程中每个设备只用和邻居通信，因此发送的数据总量大致是 $ 2M $，和 $ N $ 无关，很适合大规模的集群训练，不会因为加卡而出现单卡通讯瓶颈。
The Memory Wall
虽然通信问题得到了解决，但是随着模型参数量逐渐加大，单卡的显存也成为了瓶颈。传统数据并行方案中每张卡都要存储完整的模型和状态，随着参数量增大，不可能跑得动大模型。
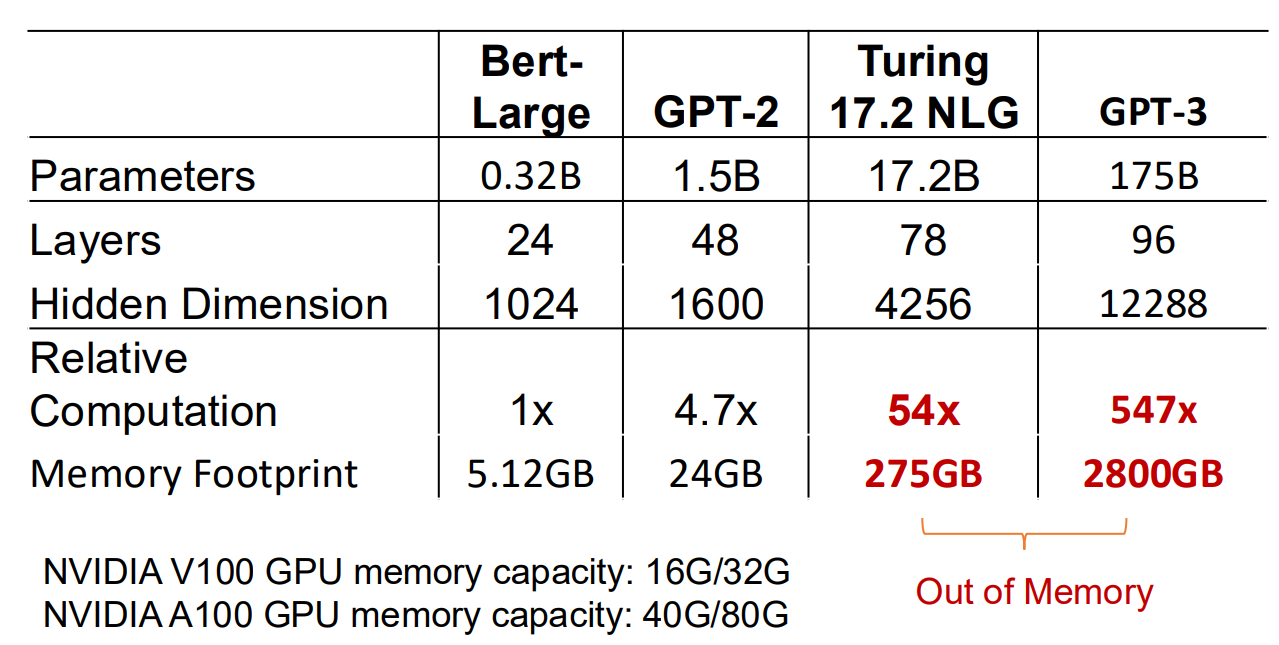
想要解决这个问题，首先需要知道显存到底被谁消耗了？实际上除了模型权重本身，还有更多的显存消耗在了梯度和优化器状态上。
真实的训练过程中，为了确保精度的同时加速计算，通常会采用混合精度的方法，同时维护 FP16 和 FP32 两种格式的数据。
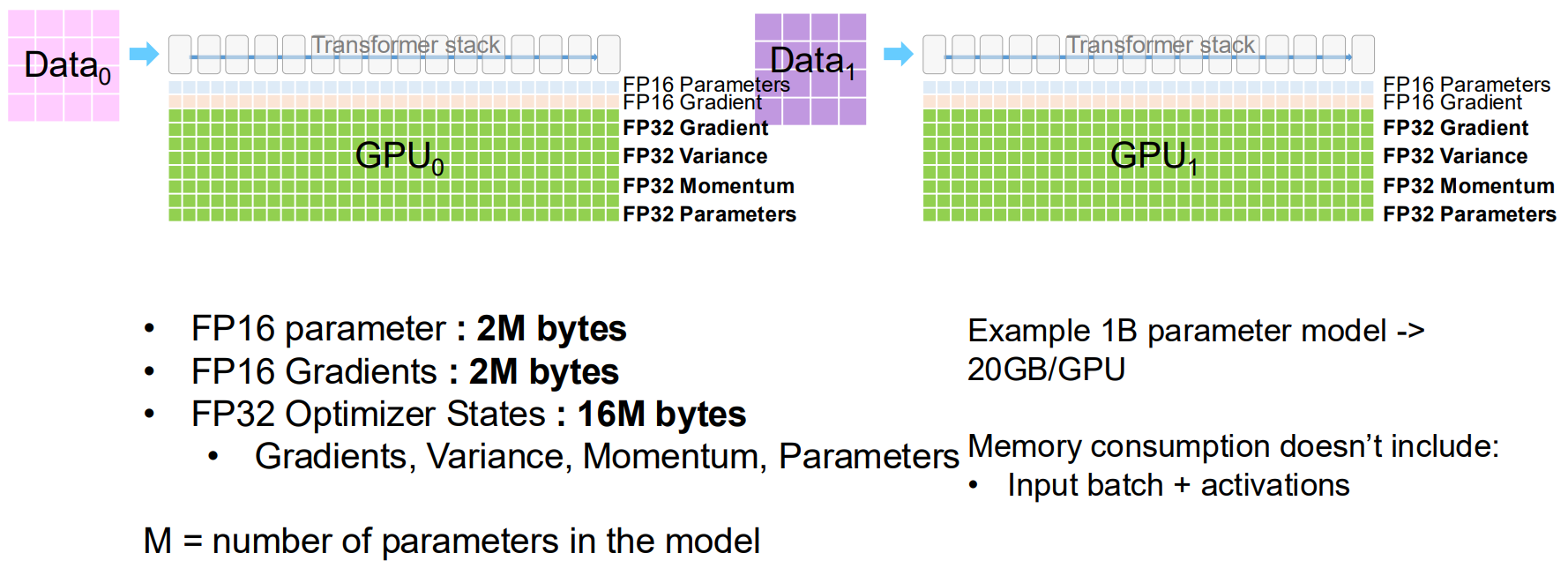以 1B 的模型为例，FP16 的参数显存占用 $ 1 \text{B} \times 2 \text{ bytes} = 2 \text{GB} $；FP16 的梯度显存占用 $ 1 \text{B} \times 2 \text{ bytes} = 2 \text{GB} $；FP32 的优化器状态（为了数值的稳定性，一般需要更高的精度）通常包含 $ 3 $ 个 FP32 的变量，从而显存占用达到了 $ 16\text{GB} $。从而光是加载这么一个模型，就已经占用了 $ 20\text{GB} $ 的显存。
并且在训练时，还需要保存前向传播每一层输出的结果，用于反向传播计算梯度。对于长文本训练，这里动态的显存占用也同样是一个很大的开销。
ZeRO
ZeRO 的目标就是解决上面遇到的显存问题，核心思想很简单，就是把这些通用的数据公用，分摊开销。
ZeRO 根据切分的粒度，分成了 $ 3 $ 个 Stage。
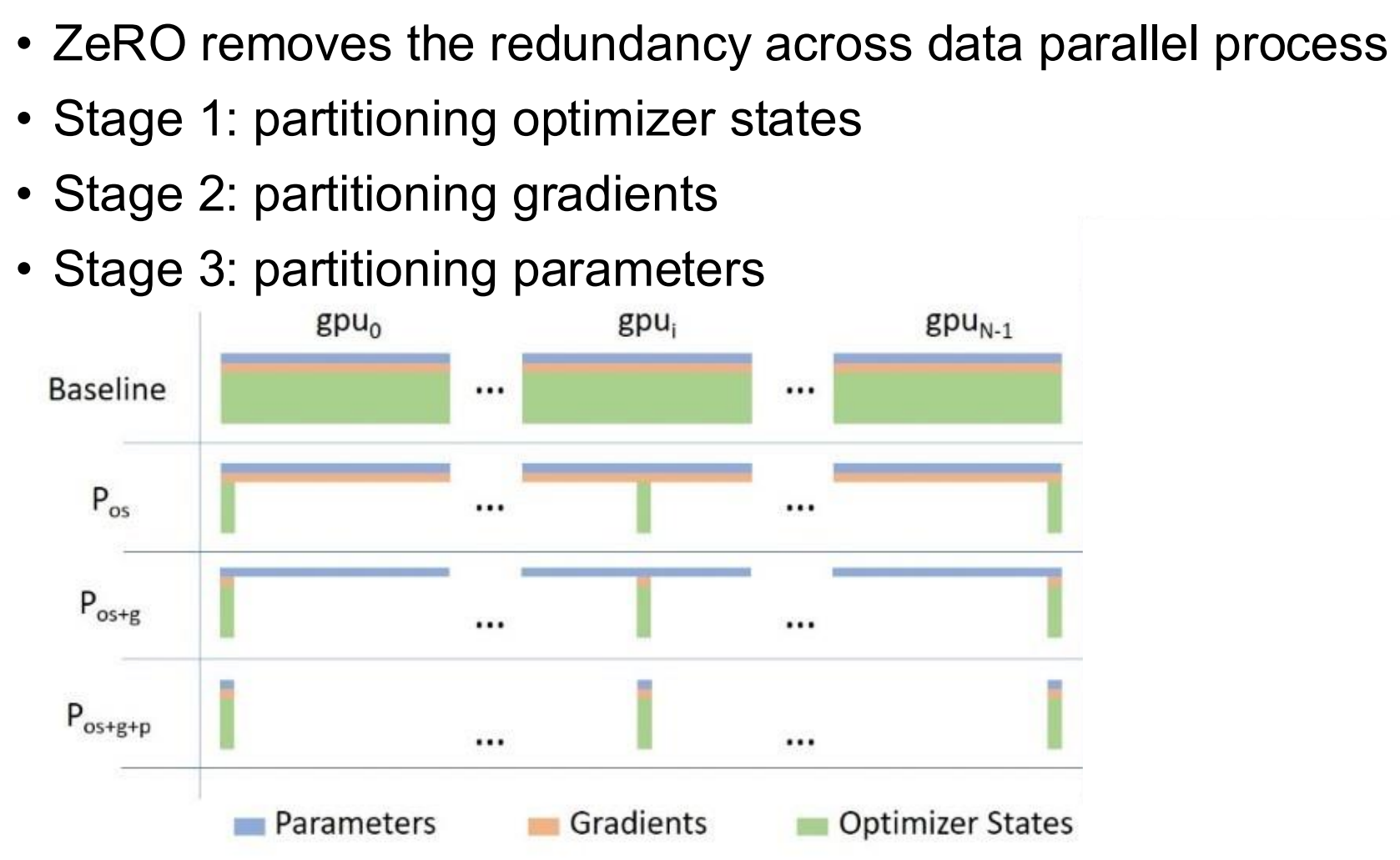
Stage 1: $ P_{\text{os}} $
切分优化器的状态。这是最直观也是性价比最高的一步。在上面的例子里，单优化器的状态就占了 $ 80\% $ 的显存，并且每张卡上存储的优化器状态时完全一样的。因此很自然就想到每张卡只负责维护 $ \frac{1}{N} $ 的优化器状态。
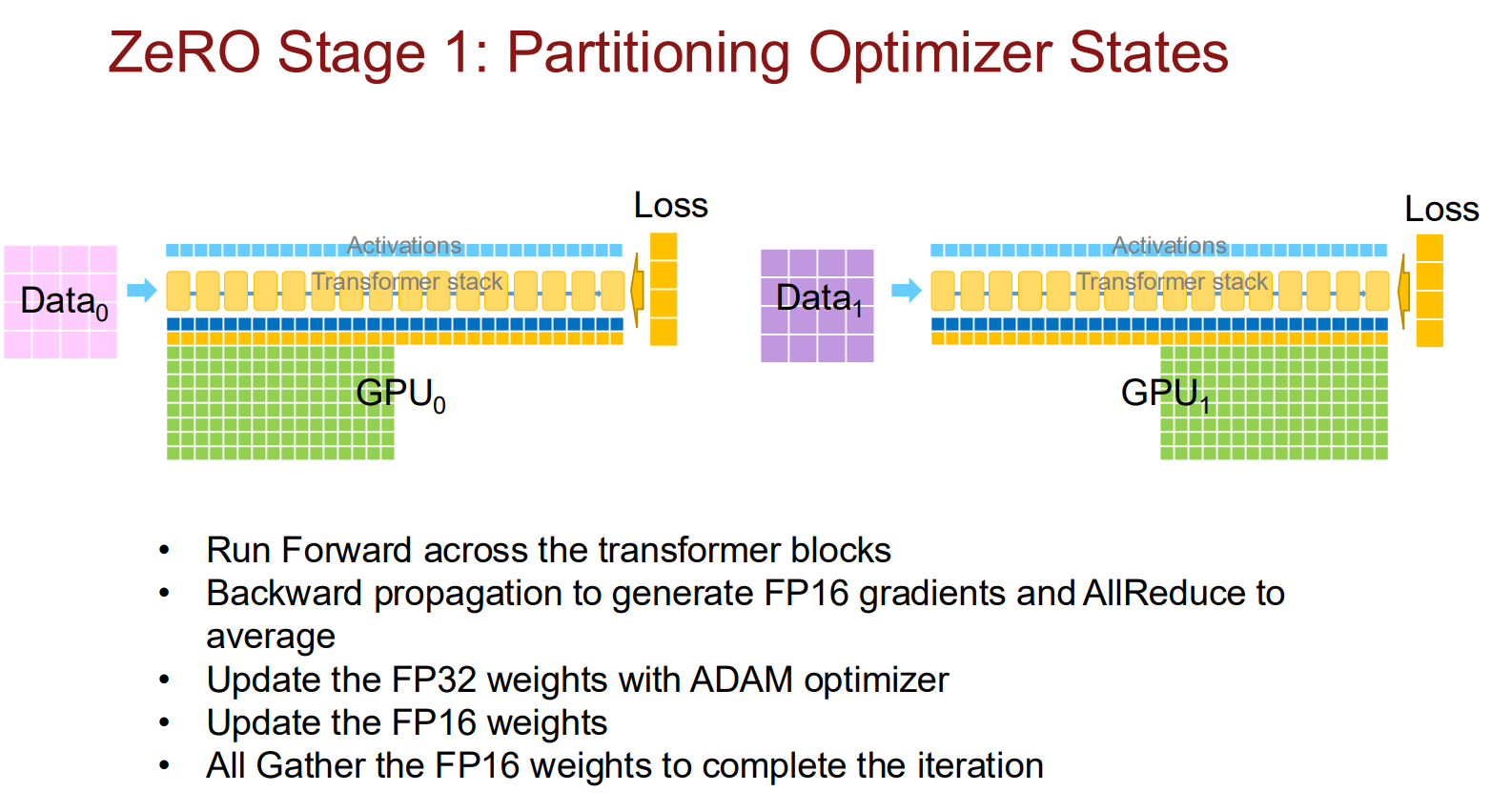
工作流程
- Forward & Backward：每张卡正常进行前向和反向传播，计算出完整的梯度。
- Scatter-Reduce：这是关键的一步。不同于传统的数据并行（直接做 All-Reduce 得到完整梯度），ZeRO Stage 1 只做 Scatter-Reduce。
- 结果：GPU 0 只需要收集并聚合第 0 块梯度的总和，GPU 1 只需要第 1 块… 以此类推。
- 注：此时每张卡手里只有它负责的那一小块平均梯度。
- Optimizer Step：GPU $ k $ 使用它持有的那 $ \frac{1}{N} $ 块平均梯度，去更新它显存里维护的那 $ \frac{1}{N} $ 块优化器状态和模型参数。
- All-Gather：现在每张卡上的模型参数只有 $ \frac{1}{N} $ 是最新的。为了进行下一轮训练，大家立刻执行 All-Gather，将各自更新好的参数广播给所有设备。
收益与代价
- 显存：节省了巨大的 FP32 状态显存。
- 通信：通信量没有增加。原本的 Ring AllReduce 分为 Scatter-Reduce + All-Gather 两个阶段。ZeRO Stage 1 只是把这两个阶段拆开了，先做 Scatter-Reduce 拿到梯度，更新完参数后，再做 All-Gather。总量依然是 $ 2 \times M $。
Stage 2: $ P_{\text{os+g}} $
既然已经切了优化器状态，同样梯度也一样可以切。原理是每张卡不再保存完整的梯度，只保存它负责更新的那 $ 1/N $ 的梯度，这样又节省了梯度的显存占用。（和 Stage 1 的区别是显式增加了梯度部分缓存的释放）
工作流程
- Backward：算出梯度后，立刻进行 Reduce-Scatter 操作。
- Reduce-Scatter：互相传阅梯度，最后每块 GPU 只保留自己负责的 $ \frac{1}{N} $ 块梯度和。
- 释放显存：其他部分的梯度在 Reduce-Scatter 之后就可以立刻扔掉（释放显存），不需要一直存着。
收益：进一步节省了显存，通信量依然保持不变。
Stage 3: $ P_{\text{os+g+p}} $
更加激进的一步，连着参数一起切分，每张卡上不再有完整的模型。原理是前向传播时“用时再取”，用通信量换取显存。
工作流程
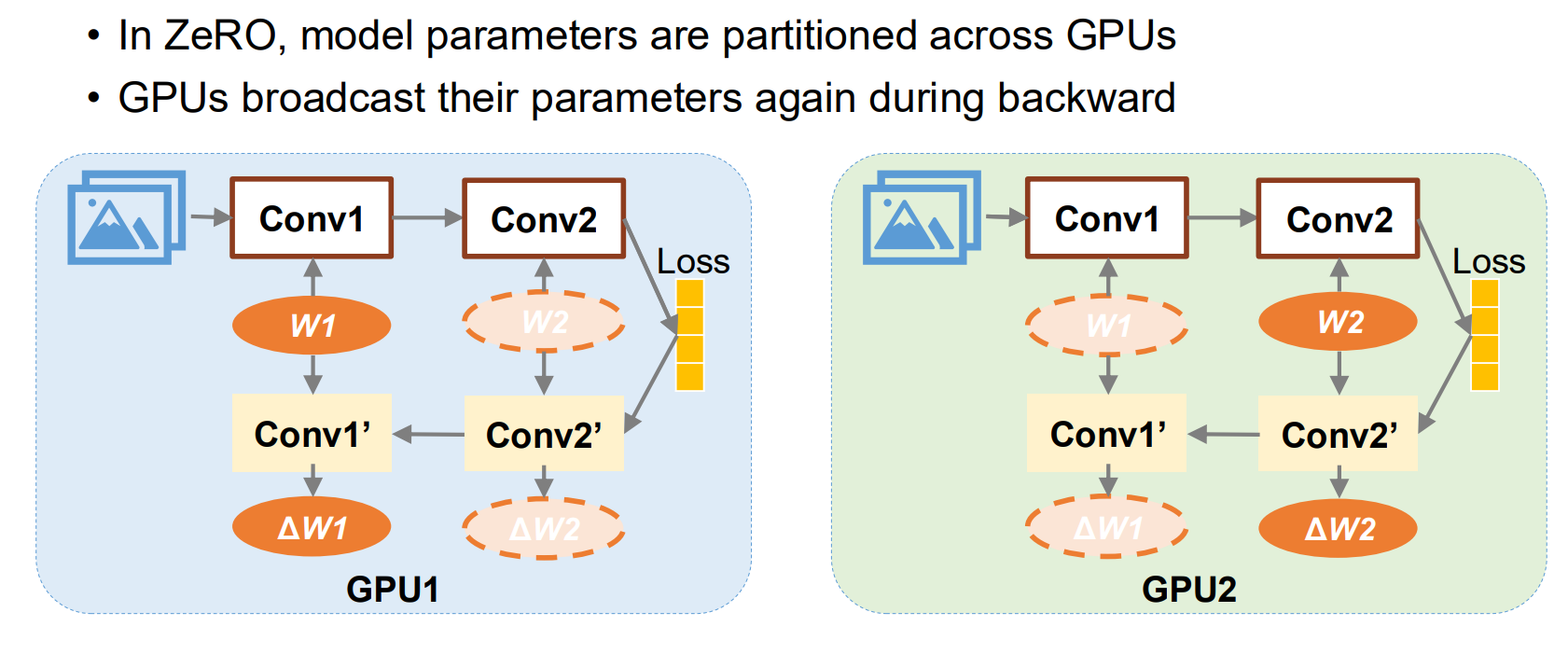
- Forward:
- 当 GPU 要计算第 1 层 (Conv1) 时，每个设备只有 Conv1 的一小块碎片。
- Action：立刻发起一次 All-Gather，把自己手里的 Conv1 碎片拼起来。
- Compute：拼好完整的 Conv1 后，进行计算。
- Discard：算完 Conv1，立刻把借来的参数扔掉，只保留自己负责的那一小块碎片，释放显存。
- 接着算 Conv2… 重复上述过程。
- Backward:
- 反向传播时同理。要算 Conv2 的梯度，再次 All-Gather 拼出完整的 Conv2 参数，算完梯度后再次扔掉。
收益与代价
- 显存：显存占用降到了极致。随着 GPU 数量 N 增加，单卡显存占用线性下降。理论上你可以训练无限大的模型。
- 通信：通信量增加了 50% (1.5x)。因为每次前向和反向都要重新 All-Gather 参数，比之前多了一次全量的参数广播。
Summary
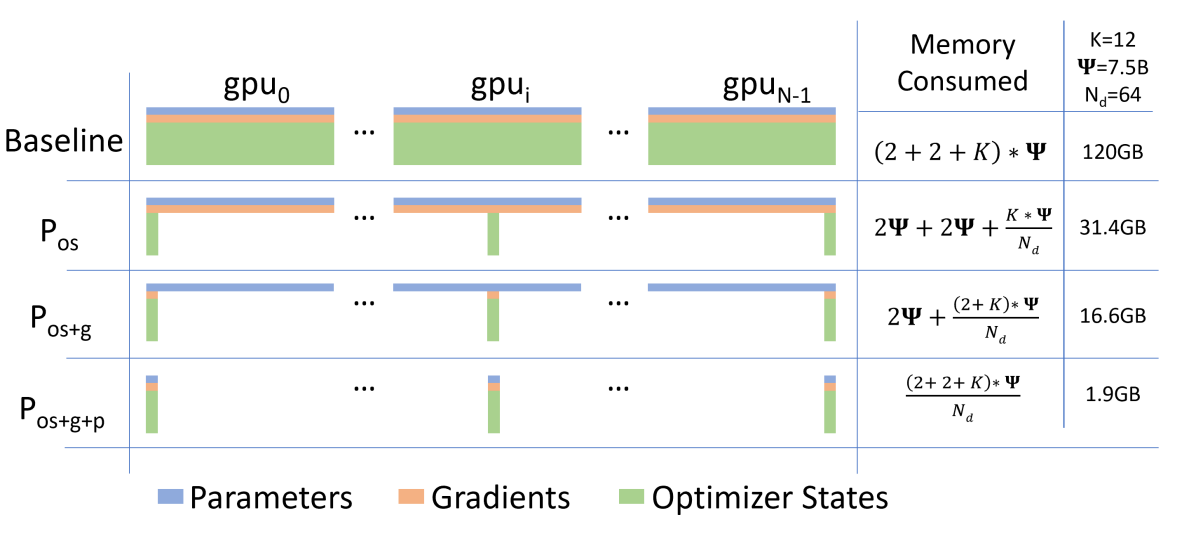在 64 卡的设置下，ZeRO-3 能把单卡显存占用从 120GB 压到 1.9GB。
在 PyTorch 中，这个技术对应的是 FSDP (Fully Sharded Data Parallel)。
本质就是在 Compute (计算)、Memory (显存) 和 Communication (通信) 这三者之间做 Trade-off。