Problem 1
证明存在常数 $ c > 1 $ 和 $ N > 0 $,使得当 $ n > N $ 时, $ [n] $ 上树的同构类数量至少为 $ c^n $ 。
证
我们需要的同构类的数量则可以看成 $ n $ 个点无标号的树的数量。需要证明这个数量增长的足够快。
首先根据 Cayley 公式,$ n $ 个点的有标号的树的数量为 $ n^{n-2} $。显然所有无标号的树的数量大于 $ \dfrac{n^{n-2}}{n!} $,因为这里直接假设所有点都是对称的,但是实际上一棵有标号的树并不会对应 $ n! $ 颗无标号的树。我们直接取 $ c=2 $,于是就只需要证明存在 $ N>0 $ 满足在 $ n>N $ 时有 $$ \dfrac{n^{n-2}}{n!} > 2^{n} $$ 我们使用斯特林公式,在 $ n $ 足够大时有 $$ n! \approx \sqrt{ 2\pi n }\left( \dfrac{n}{e} \right)^{n} $$ 带入下界,得到 $$ \dfrac{n^{n-2}}{n!} \approx \dfrac{e^{n}}{\sqrt{ 2\pi}\cdot n^{5 / 2}} $$ 所以只需要证明在 $ n>N $ 时有 $$ (\sqrt{ 2\pi })^{1 / n} \cdot n^{5 / 2n} < \dfrac{e}{2} $$ 对于左式,显然有 $$ \lim_{ n \to \infty } [(\sqrt{ 2\pi })^{1 / n} \cdot n^{5 / 2n}] = 1 < \dfrac{e}{2} $$ 根据极限的定义,我们总能找到一个 $ N $ 满足条件。因此得证!
Problem 2
- 假设 $ G $ 是 $ [n] $ 上的一个图,且 $ G \cong \overline{G} $ 。证明如果 $ n = 4k + 1 $ (其中 $ k $ 是某个整数),则存在一个度为 $ 2k $ 的顶点。
- 对于哪些 $ n $ 值,存在一个 $ [n] $ 上的图 $ G $ 使得 $ G \cong \overline{G} $ 成立?证明你的答案。
(1)
我们需要证明一个无向图和它的补图同构时,如果 $ n=4k+1 $,那么存在度数为 $ \frac{n-1}{2} $ 的顶点。
首先我们设 $ G=(V,E) $。$ G \cong \overline{G} $ 说明对于任意 $ v\in V $,均存在 $ u\in V $ 满足 $ \text{deg}(v) = (n-1)-\text{deg}(u) $(补图中所有点的度数组成的序列和原来相同)。这说明对于任意一个度数 $ d $,均存在 $ (n-1)-d $ 与之对应。
假设不存在 $ d= \frac{n-1}{2} $,那么我们就能把所有点按照度数两两配对成度数为 $ (d,n-1-d) $ 的对(因为 $ d\neq n-1-d $)。然而由于 $ n $ 是奇数,必然有一个点无法配对,因此矛盾。所以必然存在度数为 $ \frac{n-1}{2} $ 的点。
(2)
首先必须要满足 $ G $ 和 $ \overline{G} $ 的边数相等,因此 $$ \left| E \right| = \binom{ n }{ 2 } - \left| E \right| $$ 得到 $ \left| E \right|= \dfrac{n(n-1)}{4} $,从而有 $ n=4k $ 或 $ n=4k+1 $。
接着我们考虑用更形式化的方式描述 $ G \cong \overline{G} $。这等价于存在一个 $ n $ 的置换 $ \varphi:[n]\to[n] $ 满足对于所有 $ (u,v)\in E $,那么 $ (\varphi(u),\varphi(v))\not\in E $。
我们现在分别对 $ n=4k $ 和 $ n=4k+1 $ 两种情况都构造出对应的 $ G $ ,证明只要 $ n\equiv 0,1\pmod 4 $,就存在对应的 $ G $。
Case 1:若 $ n\equiv 0\pmod 4 $。我们取 $ \varphi[n]=(2,3,\dots,n,1) $,即 $ \varphi(k)=k+1\pmod n $。由于 $ n $ 为偶数,所以我们将所有点按照 $ 1,\dots,n $ 编号,可以将所有的点按照编号分成奇数和偶数两组,显然在这种构造下,令 $ G $ 包含所有两端点编号为奇数的边,比如 $ (u,v) $,必然有 $ \varphi(u,v)\not\in E $。
除此之外还需要包含一半的两端编号奇偶不同的边。若 $ i $ 为奇数,$ j $ 为偶数,我们考虑边 $ (i,j) $ 和所有端点编号之差($ \text{mod }n $)相同的边,显然对于任意 $ u\in[n] $,都能找到对应的 $ v\equiv u+(i-j)\pmod n $ 使得 $ (u,v) $ 为这样的一条边,所以我们不妨设所有的这些边为 $ (1,j_{1}),(2,j_{2}),\dots ,(n,j_{n}) $,并且这些边按照 $ \varphi $ 的调用关系形成了一个长度为 $ n $ 的环。所以我们直接在这个环上间隔地取边加入到 $ G $ 中,就构造出了正确的边集,具体而言,取 $ (2k+1,j_{2k+1}) $。对于所有的环,都用这样的方式取出一半的边加入到 $ G $,最终得到的边集 $$ E = \{ (u,v)\mid u\equiv v\equiv 1\pmod n \} \cup \{ (u,(u+t)\text{ mod }n)\mid u \in [n],t \in \{1,3,\dots,n-1 \} \} $$ 容易验证这时 $ \varphi(E)\cap E=\emptyset $ 并且 $ \varphi(E)\cup E=\binom{[n] }{ 2 } $。
Case 2:若 $ n\equiv 1\pmod 4 $。设 $ n = 4k + 1 $。将顶点集标记为 $ \{0, 1, \dots, 4k-1, \infty\} $。定义置换 $ \varphi $ 如下: $ \varphi(\infty) = \infty $,且对于 $ i = 0, 1, \dots, 4k-1 $, $ \varphi(i) = (i + 1) \mod 4k $。
该置换 $ \varphi $ 在边集上的作用将所有可能的边根据端点编号的差值划分为不同的组,每个组的大小均为偶数。具体而言:
- 与 $ \infty $ 相连的边 $ \{\infty, i\} $($ i = 0, \dots, 4k-1 $)形成一个为大小 $ 4k $(偶数)的组。
- 其余边 $ \{i, j\} $($ i, j \in \{0, \dots, 4k-1\} $, $ i \neq j $)的形成的组大小也均为偶数(取决于差异 $ d = |i - j| \mod 4k $,但均为偶数)。
对于每个组(视为 $ \varphi $ 作用下的环),选择交替的半数边加入 (即同一组中相邻边一在 $ G $ 中,一不在,确保与 $ \varphi(G) = \overline{G} $ 一致)。由于总数为偶数,此选择无矛盾,且确保 $ E \cup \varphi(E) = \binom{[n]}{2} $ 且 $ E \cap \varphi(E) = \emptyset $,从而 $ G \cong \overline{G} $。
此构造证明了当 $ n \equiv 1 \pmod{4} $ 时,存在满足条件的图 $ G $。
Problem 3
在一个连通图 $ G $ 中,如果存在不止一条最长路径,证明任意两条最长路径都共享一个共同顶点。
证
假设有两条不重合的最长路径,端点分别为 $ (s,t),(s',t') $,路径长度为 $ l $。设 $ (s,t) $ 上的顶点 $ a $ 和 $ (s',t') $ 上的顶点 $ b $ 满足 $ (a,b) $ 的最短路径 $ S $ 不属于 $ (s,t) $ 和 $ (s',t') $。我们设 $ (s,a) $ 的长度为 $ d_{1} $,$ (b,t') $ 的长度为 $ d_{2} $。
因此我们可以以此构造出 $ 4 $ 条路径:
- $ s\to a\to b\to t' $:长度为 $ d_{1}+\left| S \right|+d_{2} $。
- $ s\to a\to b\to s' $:长度为 $ d_{1}+\left| S \right|+l-d_{2} $。
- $ t\to a\to b\to t' $:长度为 $ l-d_{1}+\left| S \right|+d_{2} $。
- $ t\to a\to b\to s' $:长度为 $ l-d_{1}+\left| S \right|+l-d_{2} $。
这 $ 4 $ 条路径长度之和为 $ 4l+4\left| S \right| $,说明其平均长度为 $ l+\left| S \right|>l $,其中肯定至少有一条长度大于 $ l $ 的路径,这与 $ l $ 是最长路径矛盾!
说明不存在不重合的最长路径。
Problem 4 (Bonus)
证明或反驳:在一个连通图中,所有最长路径(如果多于一条)都共享一个共同顶点。
反例
我们考虑构造一个图满足,对于图中任意一个点都存在一条最长路径不经过这个点,这样所有最长路径的交集就是空集,可以作为一个反例。
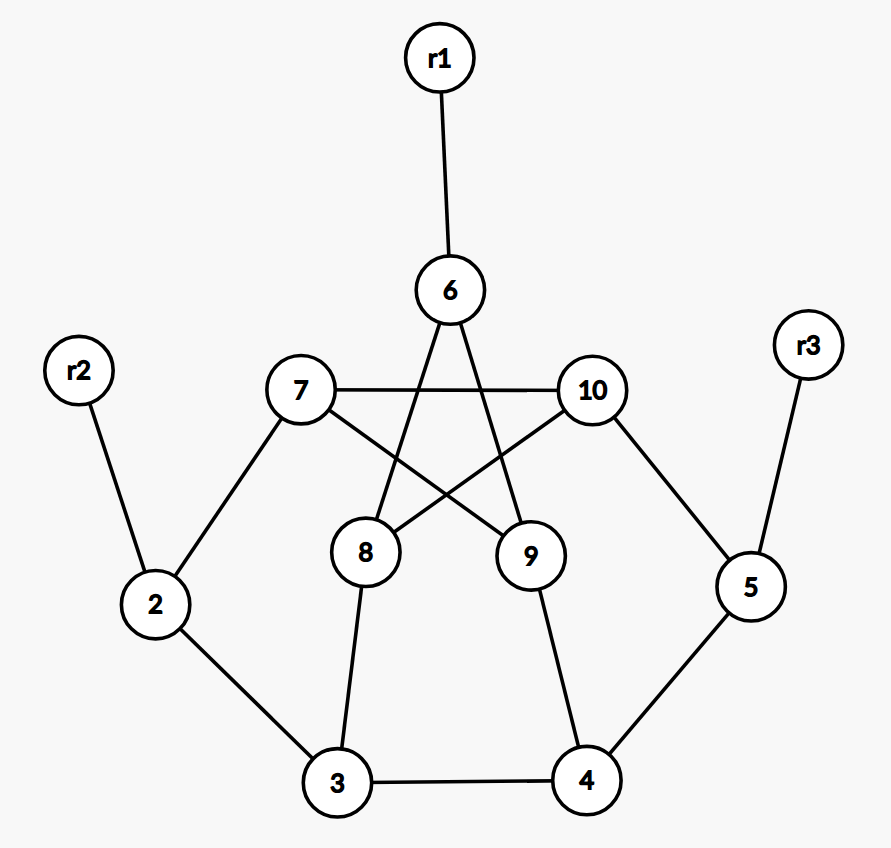
考虑这样一个图,最长路径长度为 $ 9 $,并且总共 $ 12 $ 个顶点,任意去掉一个点,都还存在经过 $ 10 $ 个点的最长路径,符合我们的构造,这就得到了一个反例。