Problem 1
(1)
证明: $$ \chi(G) + \chi(\overline{G}) \leq v(G) + 1 $$ 证
归纳证明。对于大小为 $ 1 $ 的图,结论显然成立,此时 $ \chi(G)=\chi(\overline{G})=1 $。
假设对于大小为 $ n-1 $ 的图这个结论都成立,那么对于一个大小为 $ n $ 的图 $ G $,我们考虑加入一个点 $ v $。此时我们有 $$ \chi(G-v)+\chi(\overline{G}-v) \leq n $$ 我们现在证明 $ \chi(G) $ 和 $ \chi(\overline{G}) $ 中至多只有一个可能会增加 $ 1 $。设 $ G $ 中 $ v $ 的度数为 $ d(v) $,在 $ \overline{G} $ 中为 $ \overline{d}(v)=n-1-d(v) $。
若 $ d(v)< \chi(G-v) $ 或 $ \overline{d}(v)< \chi(\overline{G}-v) $。那么在一个图中新加入的点可以直接使用原来的颜色,不会增加这个图的染色数,并且另一个图至多只会增加一种染色数。在这两种情况下,直接就能得到 $$ \chi(G)+\chi(\overline{G}) = \chi(G-v)+\chi(\overline{G}-v)+1 \leq n+1 $$
由于 $ d(v)+(n-1-d(v))=n-1 $,所以如果这两个不等式都不成立,我们就有 $$ d(v)+\overline{d}(v)=n-1\geq \chi(G-v)+\chi(\overline{G}-v) $$ 从而 $$ \chi(G)+\chi(\overline{G})\leq (\chi(G-v)+1) + (\chi(\overline{G}-v)+1) \leq n-1+2=n+1 $$
综上,我们就证明了 $$ \chi(G)+\chi(\overline{G}) \leq n+1 $$ (2)
找到一个 $ n $ 阶的图满足 $ \chi(G)\cdot \chi(\overline{G})= \frac{(n+1)^{2}}{4} $。
解
考虑 $ n $ 为奇数。
用以下方式构造出 $ G $:在 $ n $ 个点中取出 $ \dfrac{n+1}{2} $ 个点组成一个完全图,剩下 $ \dfrac{n-1}{2} $ 个点构成一个独立集。这样 $ \chi(G)=\dfrac{n+1}{2} $,因为完全图子图中每个点颜色都要彼此不同。
现在我们来考虑 $ \chi(\overline{G}) $。$ \overline{G} $ 为一个 $ \dfrac{n+1}{2} $ 部完全图,同样也有 $ \chi(\overline{G})=\dfrac{n+1}{2} $。
这是就有 $$ \chi(G)\cdot \chi(\overline{G}) = \dfrac{(n+1)^{2}}{4} $$
Problem 2
一个图 $ G $ 的最优着色是指一个仅使用 $ \chi(G) $ 种颜色的正确着色 $ \varphi $,其中 $ \chi(G) $ 是图 $ G $ 的色数。
证明或反驳:对于所有简单图 $ G $,存在一个最大独立集 $ W $ 和一个最优着色 $ \varphi $,使得 $ W $ 中至少 $ |W|/4 $ 个顶点被 $ \varphi $ 分配了相同的颜色。
反例
构造一下反例:
其中最大独立集大小为 $ 5 $,取外圈的一层点,但是 $ \chi(G)=5 $,最大独立集中每个点都被染上了不同的颜色,与题设矛盾。
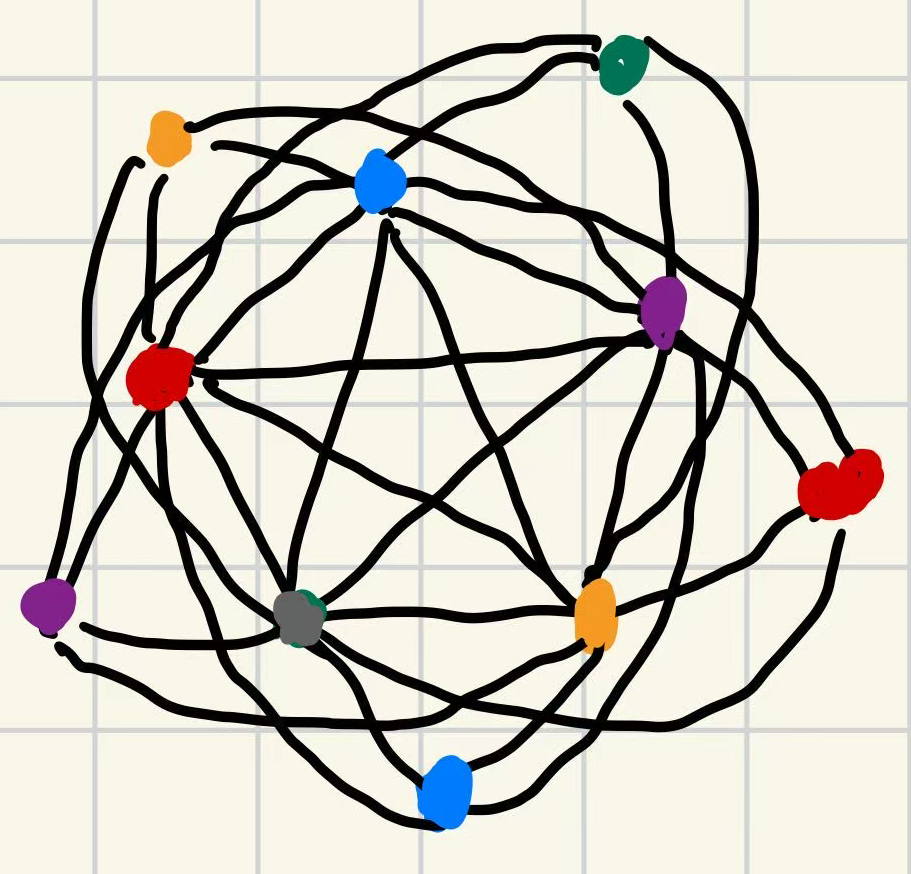
构造思路:先用中间的团来限制染色数为 $ 5 $,接着再向外拓展其他的点,保证这些点构成独立集,并且颜色被限定只能与对面的点相同。
注:本题并非独立解决,经过了和同学的讨论后才作出。
Problem 3
证明:如果一个二部图 $ G = (L, R, E) $ 满足 $ |L| = |R| = n $ 且没有完美匹配,则存在一个集合 $ S $ 使得:
(i) $ |S| = |N(S)| + 1 $,其中 $ N(S) $ 是 $ S $ 的所有邻居集合;
(ii) $ |S| \leq \lceil n/2 \rceil $;
(iii) $ N(S) $ 中的每个顶点在 $ S $ 中至少有两个邻居。
证
由于二部图 $ G = (L, R, E) $ 满足 $ |L| = |R| = n $ 且没有完美匹配,根据 Hall 婚姻定理,存在 $ S \subseteq L $ 使得 $ |N(S)| < |S| $,并且也同样存在 $ S\subseteq R $ 使得 $ \left| N(S) \right|<\left| S \right| $。
我们设 $ S_{L} $ 为所有 $ L $ 满足条件的子集中顶点数最少的那个,$ S_{R} $ 为所有 $ R $ 满足条件的子集中顶点数最少的那个。
我们证明 $ S_{L} $ 满足性质 $ (1) $,$ S_{R} $ 同理。显然此时 $ \left| S_{L} \right|\geq \left| N(S_{L}) \right|+1 $,我们此时只需要证明 $$ \left| S_{L} \right| \leq \left| N(S_{L}) \right| +1 $$ 从 $ S_{L} $ 中任意删掉一个顶点,此时会得到一个规模小于 $ S_{L} $ 的集合 $ S^{*} $。由于 $ S_{L} $ 是最小的满足条件的子集,因此对于 $ S^{*} $ 有 $$ \left| S^{*} \right| = \left| S_{L} \right| - 1 \leq \left| N(S^{*}) \right| \leq \left| N(S_{L}) \right| $$ 这样就得到了 $$ \left| S_{L} \right| \leq \left| N(S_{L}) \right| +1 $$ 从而得到 $ S_{L} $ 满足性质 $ (1) $ $$ \left| S_{L} \right| =\left| N(S_{L}) \right| + 1 $$
接着证明 $ S_{L} $ 满足性质 $ (3) $。在性质 $ (1) $ 的证明中我们还可以发现必然有 $ \left| N(S^{*}) \right|=\left| N(S_{L}) \right| $(将结论代回 $ S^{*} $ 的不等式即可),说明 $ S_{L} $ 中任意删掉一个顶点都不会减少它的邻居数量,显然这就得到了 $ N(S_{L}) $ 中的每个点都有至少两个邻居,也就是 $ S_{L} $ 中每个点不会独占一个邻居。
因此 $ S_{L} $ 和 $ S_{R} $ 都满足性质 $ (1),(3) $。下面我们证明它们中至少有一个满足性质 $ (2) $。
我们构造 $ T=R\setminus N(S_{L}) $,显然有 $ N(T)\subseteq L\setminus S_{L} $。我们计算 $ \left| T \right| $ 和 $ \left| N(T) \right| $ 的大小,得到 $$ \left| T \right| = n - \left| S_{L} \right| +1, \left| N(T) \right| =n-\left| S_{L} \right| $$ 由于 $ N(T)< \left| T \right| $,我们知道 $ T $ 也是一个不满足条件的子集,于是根据 $ S_{R} $ 的最小性,得到 $$ \left| T \right| =n - \left| S_{L} \right| +1 \geq \left| S_{R} \right| $$ 从而 $$ \left| S_{L} \right| +\left| S_{R} \right| \leq n+1 $$ 其中至少有一个会满足性质 $ (2) $ $$ \left| S \right| \leq \left\lceil \dfrac{n}{2} \right\rceil $$ 证毕。
Problem 4
设 $ S $ 是集合 $ [m n] $。我们将 $ S $ 分割成 $ m $ 个大小为 $ n $ 的集合 $ A_1, \dots, A_m $。假设存在另一个将 $ S $ 分割成 $ m $ 个大小为 $ n $ 的集合 $ B_1, \dots, B_m $。证明 $ A_1, \dots, A_m $ 可以重新编号,使得 $ A_i \cap B_i \neq \emptyset $ 对于所有 $ i $。
证
我们可以很自然地把这个问题转化成一个二分图匹配问题。设有顶点集 $ L,R $,分别代表 $ A_{1},\dots A_{m} $ 和 $ B_{1},\dots,B_{m} $。我们定义 $ u_{i}\in L $ 和 $ v_{j}\in R $ 存在变当且仅当 $ A_{i}\cap B_{j}\neq \emptyset $。这样原问题就等价于证明这样构建的二分图 $ G $ 存在一个完美匹配。
我们考虑证明 $ G $ 满足 Hall 婚姻定理的条件。证明对于 $ L $ 的任意子集 $ S\subseteq L $,其邻居集合 $ N(S)\subseteq R $,需要满足 $$ \left| S \right| \leq \left| N(S) \right| $$ 我们现在任取一个非空子集 $ S\subseteq L $,假设 $ \left| S \right|=k $,对应集合 $ A_{i_{1}},A_{i_{2}},\dots,A_{i_{k}} $。它们的并集 $ U $ 大小为 $ n\times k $,设有 $$ U = \bigcup_{s \in S}A_{s} $$ 现在考虑 $ N(S) $ 集合。如果顶点 $ v_{j}\in R $ 不属于 $ N(S) $,即 $ v_{j}\not\in N(S) $,这说明 $ \forall u_{i}\in S,A_{i}\cap B_{j}=\emptyset $,说明 $ B_{j} $ 与并集 $ U $ 没有交集。这说明了 $$ U\subseteq \bigcup_{s \in N(S)}B_{s} $$ 设 $ \left| N(S) \right|=r $,那么 $ N(S) $ 中所有 $ B $ 集合的并大小为 $ n\times r $,于是根据包含关系,我们得到了 $$ n\times k \leq n\times r \implies k \leq r $$ 从而证明了 $ \left| S \right|\leq \left| N(S) \right| $,Hall 条件成立,存在完美匹配。证毕。