Introduction
条件概率指一个事件在另一个事件发生的条件下发生的概率,用记号 $ \mathbb{P}(A|B) $ 表示,仅在 $ \mathbb{P}(B)>0 $ 时有定义: $$ \mathbb{P}(A|B) = \dfrac{\mathbb{P}(A \cap B)}{P(B)} $$ 可以写成 $$ \mathbb{P}(A \cap B) = \mathbb{P}(B)\cdot \mathbb{P}(A|B) $$
对于 $ n $ 个事件,连续使用上式,即可得到 $$ \mathbb{P}\left( \bigcap_{i=1}^{n}A_{i} \right) = \prod_{k=1}^{n} \mathbb{P}\left( A_{k}\bigg|\bigcap_{i=1}^{k-1}A_{i} \right) $$ 这个式子被称为 链式法则。
Independence
对于事件 $ A,B $,如果 $ \mathbb{P}(A\cap B)=\mathbb{P}(A)\mathbb{P}(B) $,或者等价地 $ \mathbb{P}(A|B)=\mathbb{P}(A) $,那么我们称 $ A $ 和 $ B $ 是独立的。这表明 $ A $ 或 $ B $ 自己是否发生对对方是否发生没有影响。
推广到 $ n $ 个事件上有:对于事件 $ A_{1},\dots,A_{n} $,如果他们是相互独立的,说明对于任意的 $ I\subseteq[n] $ ,有 $$ \mathbb{P}\left( \bigcap_{i\in I}A_{i} \right) = \prod_{i\in I}\mathbb{P}(A)_{i} $$ 这个定义非常强,因为它要求对于所有的 $ I\subseteq[n] $ 都成立。
如果把定义改成只要求 $ I\in \binom{ [n] }{ 2 } $,可以得到两两独立的定义。
目前这都是关于有限集的定义,对于无穷多个事件 $ \{ A_{j} \}_{j\in J} $(这要求 $ J $ 是可数集,否则概率没有定义),我们说它们是互相独立的,当且仅当对于 $ J $ 的任意一个有限子集 $ I $,$ \{ A_{i} \}_{i\in I} $ 相互独立。
Law of Total Probability
假设事件 $ B_{1},B_{2},\dots,B_{n}\in \mathcal{F} $ 构成了样本空间的一个划分,即 $ \Omega=\bigcup_{i=1}^{n}B_{i} $ 并且对于 $ i\neq j $,有 $ B_{i}\cap B_{j}=\emptyset $。根据集合论的知识,我们可以推导出对于任意集合 $ A $,$ A\cap B_{i} $ 也构成了 $ A $ 的一个划分。如果我们取 $ A\in\mathcal{F} $,根据概率论公理,我们有 $$ \mathbb{P}(A) = \mathbb{P}\left( \bigcup_{n\geq 1}(A\cap B_{n}) \right) = \sum_{n\geq 1} \mathbb{P}(A\cap B_{i}) $$ 这就得到了 全概率公式。写成条件概率的形式,可以得到 $$ \mathbb{P}(A) = \sum_{n\geq 1}\mathbb{P}(B_{n})\mathbb{P}(A|B_{n}) $$
Some Examples
无限悖论
假设有无穷个球,用 $ k=1,2,\dots $ 来编号,并有一个无穷大的箱子。考察“放球”和“拿球”的过程。
放球过程表述为:对于 $ n=0,1,2,\dots $,在 12 点前的 $ 2^{-n} $ 分钟放入编号为 $ 10n+1,10n+2,\dots,10(n+1) $ 的球。
我们再使用不同的方式把球拿出来(假设拿和放都在瞬间完成):
12 点前 $ 2^{-n} $ 分钟放完球后,从箱子里拿出 $ 10(n+1) $ 号球。
这种情况下 12 点时箱子里会有无穷的球,因为编号不是 10 的倍数的球都没有被拿出来。
12 点前 $ 2^{-n} $ 分钟放完球后,从箱子里拿出 $ (n+1) $ 号球。
此时 12 点时箱子里一个球都没有,因为每个球都能找到一个对应的时刻被拿出来。
我们可以发现同样是拿一个球,最后的效果居然完全不同。我们现在考虑,如果随机拿出一个球又会怎么样?
12 点前 $ 2^{-n} $ 分钟放完球后,从箱子里均匀随机地拿出一个球。
我们计算每个球在 12 点的时候留在箱子里的概率。以 1 号球为例,其余类似。对于每个 $ n $,用事件 $ A_{n} $ 表示在 $ n $ 轮操作后 1 号球还在箱子里这个事件。我们需要关注的是 $$ A_{\infty} := \bigcap_{n\geq 0}A_{n} = \lim_{ n \to \infty } A_{n} $$ 根据上一节中概率测度的连续性,我们有 $ \mathbb{P}(\lim_{ n \to \infty }A_{n})=\lim_{ n \to \infty }\mathbb{P}(A_{n}) $。因此只需要计算 $ \mathbb{P}(A_{n}) $ 即可。我们再定义一个事件 $ B_{n} $ 表示第 $ n $ 轮拿出来的不是 1 号球,则有 $ A_{n}=B_{0}\cap B_{1}\cap\dots \cap B_{n} $。使用链式法则,就可以得到 $$ \mathbb{P}(A_{n}) = \mathbb{P}\left( \bigcap_{i=1}^{n}B_{i} \right) = \prod_{k=0}^{n}\mathbb{P}\left( B_{k}\bigg|\bigcap_{i< k}B_{i} \right) $$ 其中事件 $ B_{k}|\bigcap_{i< k}B_{i} $ 有非常明显的组合意义,显然这个概率是 $ 1- \dfrac{1}{9(k+1)+1} $。
因此 $$ \mathbb{P}(A_{n}) = \prod_{k=0}^{n} \left( 1 - \dfrac{1}{9(k+1)+1} \right) \leq e^{ -\sum_{k=0}^{n} 1/(9k+10) } $$ 由于级数 $ \sum_{k=0}^{n} \frac{1}{9k+10} $ 发散,所以 $ \lim_{ n \to \infty }\mathbb{P}(A_{n})=0 $,所以 12 点时 1 号球还在箱子里的概率 $ \mathbb{P}(S_{1}) $ 为 0。类似地,还能得到其他球的概率 $ \mathbb{P}(S_{n})=0 $。我们现在需要知道 12 点时箱子里还有球的概率,即 $ \mathbb{P}(\exists n \subset \mathbb{N},S_{n}) $,利用上一节的 union-bound,可以得到 $$ \mathbb{P}(\exists n \subset \mathbb{N},S_{n}) \leq \sum_{n\geq 1}\mathbb{P}(S_{n})=0 $$
Karger 最小割算法
一个经典的问题是求图上的最小割。给定一个连通无向图 $ G(V,E) $,我们说边集 $ C \subseteq E $ 是一个割,当且仅当删掉 $ C $ 以后剩下的 $ G(V,E\setminus C) $ 是不连通的。我们需要寻找图上最小的一个割。
我们在此处考虑用一个随机算法求解这个问题。
定义图上的缩边操作:给定 $ e=\{ u,v \}\in E $,我们将 $ u,v $ 合并成一个点,并删掉这条边,把缩完之后的图记为 $ G / e $。
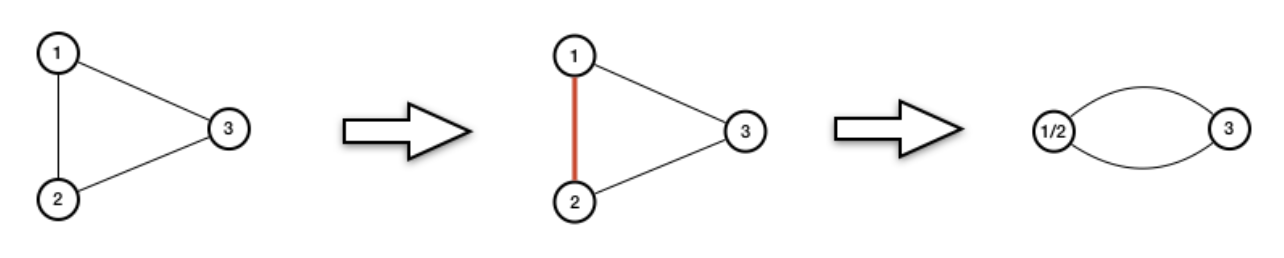
Kager 算法的原理非常简单,从 $ G $ 出发,每次随机选择一条边,把它缩掉,重复执行 $ n-2 $ 之后图里面就会只剩下两个点,这时我们再输出所有剩下的边。
这个算法“有可能”输出省却答案的原理是,由于我们关心的是”最小”的割,那么我们每一步选到割中的边的概率就不会太大。为了谈论这个概率,我们需要选择合适的概率空间。一个自然的想法是选择算法执行过程中所有删除的边的序列作为样本空间。
设 $ C $ 是一个固定的最小割,并且其大小为 $ k $,我们需要计算最终输出 $ C $ 的概率。这需要我们执行的过程中,每一次都没有选到 $ C $ 中的边。我们用 $ A_{k} $ 来表示第 $ k $ 次执行完缩边操作后,$ C $ 中的任意一条边还没有被删掉的概率。
为了分析 $ \mathbb{P}(A_{k}) $,同理上一个例子中的想法,我们定义 $ B_{k} $ 为第 $ k $ 次缩边选择的不是 $ C $ 中的边这一事件,那么显然有 $ A_{k}=\bigcap_{i=1}^{k}B_{i} $,因此根据链式法则,我们有 $$ \mathbb{P}(\text{output}=C) = \mathbb{P}(A_{n-2}) = \prod_{i=1}^{n-2}\mathbb{P}\left(B_{i}\bigg| \bigcap_{j=1}^{i-1}B_{j}\right) $$ 我们需要找出一个这个概率的下界。我们想要说明每一轮都有比较大的概率选不到 $ C $ 中的边,由于选取是均匀的,所以只需要证明在第 $ i $ 轮,已知前 $ i-1 $ 轮都没有选到 $ C $ 中的边的情况下,图中剩下的边足够多即可。
一个重要的观察是,此时图中每个点的度数都不小于 $ k $。原因是由于缩边这种操作不会破坏割的性质,如果有点的度数小于 $ k $,在原图中直接取这些边就得到了一个小于 $ k $ 的割。
有了这个观察,我们就知道在第 $ i-1 $ 轮,剩下 $ n-i+1 $ 个顶点时,至少还有 $ \frac{k}{2}\cdot(n-i+1) $ 条边,所以我们就有 $$ \mathbb{P}\left( B_{i}\bigg|\bigcap_{j=1}^{i-1}B_{j} \right) \geq 1 - \dfrac{k}{\frac{k}{2} \cdot (n-i+1)} = \dfrac{n-i-1}{n-i+1} $$ 这说明 $$ \mathbb{P}(A_{n-2}) \geq \prod_{i=1}^{n-2} \dfrac{n-i-1}{n-i+1} = \dfrac{2}{n(n-1)} $$ 因此我们的算法至少有 $ \frac{2}{n(n-1)} $ 的概率可以输出 $ C $。如果我们重复这个算法 $ N=50n(n-1) $ 次,并且输出这么多次中找到的最小的割,那么这个割是最小割的概率至少有 $$ 1-\left( 1- \dfrac{2}{n(n-1)} \right)^{N} \geq 1 - e^{ -100 } $$ 使用并查集来维护的话,复杂度大约为 $ O(n^{2}m) $。