本文简要介绍通用矩阵乘(GEMM,General Matrix Multiplication)优化的基本概念和方法。GEMM 是 HPC 领域中最基础且计算密集型的工作负载之一。在人工智能、科学模拟和图像处理等领域,它的性能直接影响着整个应用程序的效率。虽然其数学概念简单,但高效的 GEMM 实现却需要对计算机体系结构有深刻的理解,包括缓存、SIMD 指令集和并行化技术。
Naive GEMM#
GEMM 通常定义为 $ C = A \times B $,对于矩阵 $ A \in \mathbb{R}^{M \times K} $,矩阵 $ B \in \mathbb{R}^{K \times N} $,其乘积矩阵 $ C\in \mathbb{R}^{M \times N} $ 可以表示为
$$
C_{i,j} = \sum_{k=0}^{K-1} A_{i,k}\times B_{k,j}
$$
对应的朴素代码通常如下(默认行主序存储):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void gemm_naive(int M, int N, int K, const float* A, const float* B, float* C) {
for (int i = 0; i < M; ++i) {
for (int j = 0; j < N; ++j) {
C[i][j] = 0.0f; // 初始化 C[i][j]
}
}
for (int i = 0; i < M; ++i) {
for (int j = 0; j < N; ++j) {
for (int k = 0; k < K; ++k) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
}
|
分析:
浮点运算总数(FLOPs):
- 对于每个 $ C_{i,j} $ 元素,需要执行 $ K $ 次乘法和 $ K $ 次加法。
- 总共有 $ M \times N $ 个 $ C_{i,j} $ 元素。
- 总操作数约为 $ 2 \times M \times N \times K $ 次浮点运算。
内存访问总数:忽略循环变量和指令的开销。
- 矩阵 $ C $ 的初始化需要 $ M \times N $ 次写入;循环中矩阵 $ A $ 和矩阵 $ B $ 分别被读取 $ M \times N \times K $ 次,矩阵 $ C $ 被读取和写入共 $ 2 \times M \times N \times K $ 次。
- 总内存访问次数约为 $ 4 M N K + M N $。
Why Slow?#
尽管代码简洁,但这种实现方式存在严重的性能瓶颈:
对这样的矩阵乘的算法优化可分为两类:
数学角度的优化暂且不在本文的讨论范围内,有机会将单独介绍,下面给出计算机体系结构角度的一些优化角度。
1 × 4 Register Blocking#
参考 how to optimize gemm 一文,我们把输出的计算按照列拆分成若干个 $ 1 \times 4 $ 的小块,通过一次性处理 $ C $ 的一小块内存来减少内存操作,最大化寄存器的利用率。
与其一次计算 $ C_{i,j} $ 一个元素,不如一次性计算 $ C_{i, j\sim j+3} $ 四个连续元素,这很好地利用了 $ C $ 矩阵行内的空间局部性。把这四个元素加载到寄存器,可以大大减少对主存的访问次数。
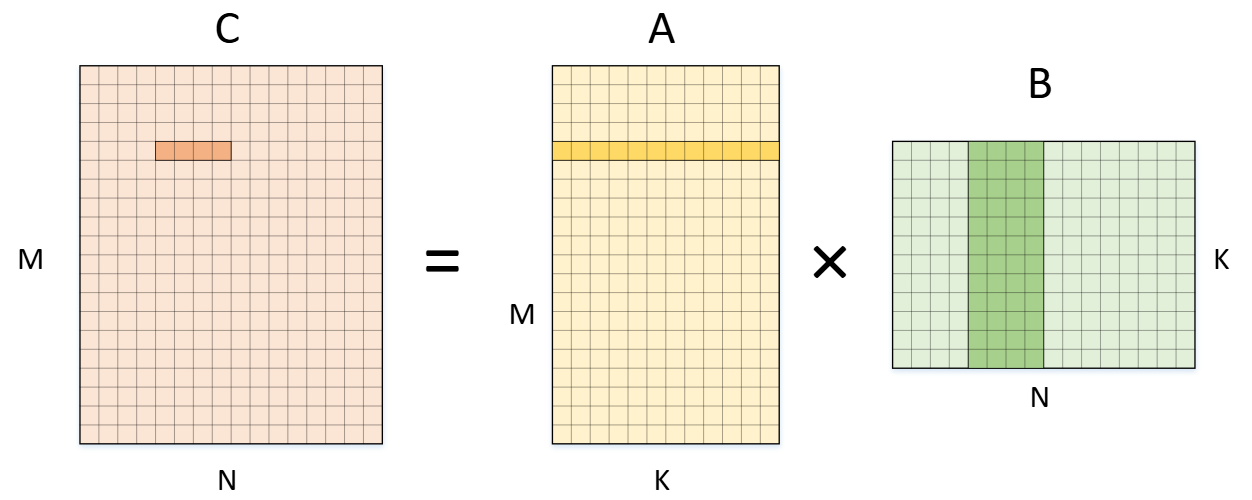
下文我们将最内层的循环称为微内核(micro kernel),比如 AddDot1x4 就是一个微内核。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| // AddDot1x4: 计算 C 的一个 1x4 块(按行主序)
// Ai 指向 A 的第 i 行起始;Bj 指向 B 的第 j 列所在的起始位置;Cij 指向 C[i][j]
inline void AddDot1x4(int K, const float* Ai, const float* Bj, float* Cij, int N) {
float c0 = 0.0f, c1 = 0.0f, c2 = 0.0f, c3 = 0.0f;
for (int k = 0; k < K; ++k) {
float a = Ai[k];
const float* bk = Bj + k * N; // B[k][j..j+3]
c0 += a * bk[0];
c1 += a * bk[1];
c2 += a * bk[2];
c3 += a * bk[3];
}
Cij[0] = c0;
Cij[1] = c1;
Cij[2] = c2;
Cij[3] = c3;
}
void gemm_1x4_blocked(int M, int N, int K, const float* A, const float* B, float* C) {
for (int i = 0; i < M; ++i) {
const float* Ai = &A[i * K];
for (int j = 0; j < N; j += 4) {
int w = std::min(4, N - j);
if (w == 4) {
AddDot1x4(K, Ai, &B[j], &C[i * N + j], N);
} else { // 处理尾部 <4 列
for (int jj = 0; jj < w; ++jj) {
float acc = 0.f;
for (int k = 0; k < K; ++k) acc += Ai[k] * B[k * N + (j + jj)];
C[i * N + j + jj] = acc;
}
}
}
}
}
|
分析:
- FLOPs:仍为 $ 2 M N K $。
- 内存访问:(以元素计,忽略缓存命中)
- 读取 $ A $:对每个 $ 1 \times 4 $ 块,每次 $ K $ 次,共 $ \frac{M N}{4} \times K = \frac{M N K}{4} $。
- 读取 $ B $:每次 $ 4K $,共 $ \frac{M N}{4} \times 4K = M N K $。
- 写入 $ C $:每块写 $ 4 $ 次,共 $ M N $。无需读取 $ C $(寄存器累加后赋值)。
- 合计:$ \frac{1}{4} M N K + 1 \cdot M N K + M N = 1.25\, M N K + M N $。
与 naive 相比,$ A $ 的读取减少了 $ 4 \times $(复用到 4 个连续列),$ B $ 的读取次数相同但连续访问更友好,$ C $ 的访存从每次迭代读写降为仅写一次。
加速比:
在内存带宽主导的 Roofline 模型 下,性能与内存访问次数近似成反比,因此加速比为
$$
S_{\text{1x4}} \approx \frac{4 M N K + M N}{1.25 M N K + M N} \approx \frac{4}{1.25} = 3.2 \quad (K \gg 1)
$$
Loop Unrolling and Pointer Optimization#
为了进一步优化,我们在 AddDot1x4 内部使用指针迭代与循环展开,减少地址计算和分支开销,提升指令级并行性与寄存器利用。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| inline void AddDot1x4_unroll4(int K, const float* Ai, const float* Bj, float* Cij, int N) {
float c0 = 0.f, c1 = 0.f, c2 = 0.f, c3 = 0.f;
const float* a = Ai;
const float* b = Bj;
int k = 0;
for (; k + 3 < K; k += 4) {
float a0 = a[0], a1 = a[1], a2 = a[2], a3 = a[3];
const float* b0 = b + 0 * N;
const float* b1 = b + 1 * N;
const float* b2 = b + 2 * N;
const float* b3 = b + 3 * N;
c0 += a0 * b0[0] + a1 * b1[0] + a2 * b2[0] + a3 * b3[0];
c1 += a0 * b0[1] + a1 * b1[1] + a2 * b2[1] + a3 * b3[1];
c2 += a0 * b0[2] + a1 * b1[2] + a2 * b2[2] + a3 * b3[2];
c3 += a0 * b0[3] + a1 * b1[3] + a2 * b2[3] + a3 * b3[3];
a += 4;
b += 4 * N;
}
for (; k < K; ++k) {
float av = *a++;
const float* bk = b; b += N;
c0 += av * bk[0]; c1 += av * bk[1]; c2 += av * bk[2]; c3 += av * bk[3];
}
Cij[0] = c0; Cij[1] = c1; Cij[2] = c2; Cij[3] = c3;
}
|
分析:
- FLOPs:仍为 $ 2 M N K $。
- 内存访问:与 $ 1 \times 4 $ 相同($ 1.25\, M N K + M N $),仅减少了地址计算和分支开销。
加速比:
- 内存主导:与 $ 1 \times 4 $ 相同,约 $ 3.2 \times $。
- 计算主导:循环展开可进一步减少指令开销,常见提升在 $ 5\% \sim 15\% $ 范围(与编译器和微架构相关)。
4 × 4 Register Blocking#
不难意识到,用一样的逻辑可以把上面的寄存器分块从 $ 1 \times 4 $ 扩展到 $ 4 \times 4 $。这样可以进一步减少内存操作,提高效率。
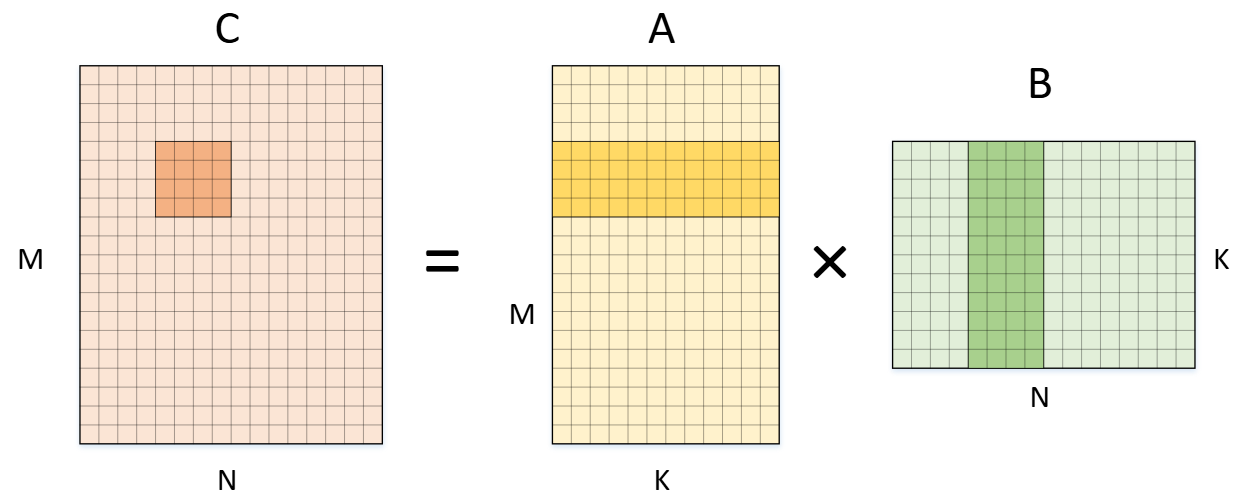
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| // AddDot4x4: 计算 C 的一个 4x4 块(行主序,传入 C 的起始为 C[i][j])
inline void AddDot4x4(int K, const float* Aij, const float* Bkj, float* Cij, int N, int Kstride) {
float
c00=0.f,c01=0.f,c02=0.f,c03=0.f,
c10=0.f,c11=0.f,c12=0.f,c13=0.f,
c20=0.f,c21=0.f,c22=0.f,c23=0.f,
c30=0.f,c31=0.f,c32=0.f,c33=0.f;
const float* a0 = Aij + 0 * Kstride;
const float* a1 = Aij + 1 * Kstride;
const float* a2 = Aij + 2 * Kstride;
const float* a3 = Aij + 3 * Kstride;
for (int k = 0; k < K; ++k) {
float a0k = a0[k], a1k = a1[k], a2k = a2[k], a3k = a3[k];
const float* bk = Bkj + k * N;
float b0 = bk[0], b1 = bk[1], b2 = bk[2], b3 = bk[3];
c00 += a0k * b0; c01 += a0k * b1; c02 += a0k * b2; c03 += a0k * b3;
c10 += a1k * b0; c11 += a1k * b1; c12 += a1k * b2; c13 += a1k * b3;
c20 += a2k * b0; c21 += a2k * b1; c22 += a2k * b2; c23 += a2k * b3;
c30 += a3k * b0; c31 += a3k * b1; c32 += a3k * b2; c33 += a3k * b3;
}
Cij[0*N+0]=c00; Cij[0*N+1]=c01; Cij[0*N+2]=c02; Cij[0*N+3]=c03;
Cij[1*N+0]=c10; Cij[1*N+1]=c11; Cij[1*N+2]=c12; Cij[1*N+3]=c13;
Cij[2*N+0]=c20; Cij[2*N+1]=c21; Cij[2*N+2]=c22; Cij[2*N+3]=c23;
Cij[3*N+0]=c30; Cij[3*N+1]=c31; Cij[3*N+2]=c32; Cij[3*N+3]=c33;
}
|
分析:
- FLOPs:仍为 $ 2 M N K $。
- 内存访问(元素计):
- 读取 $ A $:每块 $ 4K $,块数 $ \frac{M}{4}\times\frac{N}{4} $,合计 $ \frac{M N K}{4} $。
- 读取 $ B $:每块 $ 4K $,同上合计 $ \frac{M N K}{4} $。
- 写入 $ C $:每块 $ 16 $ 次,共 $ M $。
- 合计:$ 0.5\, M N K + M N $。
与 $ 1 \times 4 $ 相比,$ B $ 的读取也减少了 $ 4 \times $(同一批 $ B[k, j..j+3] $ 复用到 4 行),因此总体内存访问显著下降。
加速比:
$$
S_{\text{4x4}} \approx \frac{4 M N K + M N}{0.5 M N K + M N} \approx \frac{4}{0.5} = 8 \quad (K \gg 1)
$$
SIMD Vectorization#
现在我们引入 SIMD,以 Intel SSE 指令集为例(128-bit,单精度宽度 $ W = 4 $)。下面给出与 AddDot4x4 对齐的简化向量化微内核。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include <immintrin.h>
inline void AddDot4x4_SSE(int K, const float* Aij, const float* Bkj, float* Cij, int N, int Kstride) {
__m128 c0 = _mm_setzero_ps();
__m128 c1 = _mm_setzero_ps();
__m128 c2 = _mm_setzero_ps();
__m128 c3 = _mm_setzero_ps();
const float* a0 = Aij + 0 * Kstride;
const float* a1 = Aij + 1 * Kstride;
const float* a2 = Aij + 2 * Kstride;
const float* a3 = Aij + 3 * Kstride;
for (int k = 0; k < K; ++k) {
__m128 b = _mm_loadu_ps(&Bkj[k * N]); // B[k][j..j+3]
__m128 a0v = _mm_set1_ps(a0[k]);
__m128 a1v = _mm_set1_ps(a1[k]);
__m128 a2v = _mm_set1_ps(a2[k]);
__m128 a3v = _mm_set1_ps(a3[k]);
c0 = _mm_add_ps(c0, _mm_mul_ps(a0v, b));
c1 = _mm_add_ps(c1, _mm_mul_ps(a1v, b));
c2 = _mm_add_ps(c2, _mm_mul_ps(a2v, b));
c3 = _mm_add_ps(c3, _mm_mul_ps(a3v, b));
}
_mm_storeu_ps(&Cij[0 * N], c0);
_mm_storeu_ps(&Cij[1 * N], c1);
_mm_storeu_ps(&Cij[2 * N], c2);
_mm_storeu_ps(&Cij[3 * N], c3);
}
|
分析:
- FLOPs:仍为 $ 2 M N K $。
- 内存访问:与标量
4×4 相同($ 0.5\, M N K + M N $)。SIMD 仅改变算术吞吐,不改变 DRAM 访存量。 - 计算主导场景的理论加速:约等于向量宽度 $ W $(SSE 单精度为 $ 4 $;AVX2 为 $ 8 $;AVX-512 为 $ 16 $)。若支持 FMA(如 AVX2/FMA、AVX-512),每周期可进一步提升。
加速比:
- 内存主导:约 $ 8 \times $(同
4×4)。 - 计算主导:
4×4 与 SIMD 的收益不可直接相乘,约 $ 8 \times W $ 的上界不成立;更实际的估计是:在 4×4 将算术强度显著提升后,若仍处于计算主导,则 SIMD 可再带来 $ W \times $ 左右的额外提升。
Cache Blocking(Macro-kernel)#
尽管 SIMD 和寄存器分块(微内核)带来了巨大的性能提升,但当矩阵尺寸超出 CPU 缓存容量时,性能仍会因高昂的内存访问延迟而下降。缓存分块 (Cache Blocking) 旨在将矩阵操作分解成一系列小块操作,使这些块的数据能够长时间驻留在不同级别的缓存中(例如 L1、L2、L3),从而实现数据重用最大化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| // 缓存分块 + 4x4 微内核
void gemm_blocked_4x4(int M, int N, int K, const float* A, const float* B, float* C) {
const int MR = 4, NR = 4;
const int KC = 128; // 需按架构调优
for (int kk = 0; kk < K; kk += KC) {
int Kc = std::min(KC, K - kk);
for (int i = 0; i < M; i += MR) {
int Mb = std::min(MR, M - i);
for (int j = 0; j < N; j += NR) {
int Nb = std::min(NR, N - j);
if (Mb == MR && Nb == NR) {
AddDot4x4(Kc, &A[i * K + kk], &B[kk * N + j], &C[i * N + j], N, K);
} else { // 退化处理
for (int ii = 0; ii < Mb; ++ii)
for (int jj = 0; jj < Nb; ++jj) {
float acc = 0.f;
for (int k = 0; k < Kc; ++k)
acc += A[(i + ii) * K + (kk + k)] * B[(kk + k) * N + (j + jj)];
C[(i + ii) * N + (j + jj)] = acc + C[(i + ii) * N + (j + jj)];
}
}
}
}
}
}
|
分析:
- FLOPs:仍为 $ 2 M N K $。
- DRAM 级内存访问:(理想分块并有良好复用时)
- $ A $:每个元素从 DRAM 读入约 $ 1 $ 次,$ M K $。
- $ B $:每个元素从 DRAM 读入约 $ 1 $ 次,$ K N $。
- $ C $:每个元素从 DRAM 读写各 $ 1 $ 次,$ 2 M N $。
- 合计:$ M K + K N + 2 M N $。
通过按 $ K $ 维度切块,$ A $ 与 $ B $ 的面板在较小的 $ K_c $ 上反复被微内核复用;只要 $ K_c $、$ M_r $、$ N_r $ 选取得当,就能使复用主要发生在 L1/L2/L3 中,从 DRAM 的视角看,$ A $/$ B $ 基本只需读取一次。
加速比:
$$
S_{\text{blocked}} \approx \frac{4 M N K + M N}{M K + K N + 2 M N}
$$
当 $ M = N = K = n $ 时,有 $ S \approx \frac{4 n^3}{4 n^2} = n $,随问题规模线性增长,实际受缓存与带宽上限限制。
Data Packing#
即使有了缓存分块,如果原始矩阵的内存布局导致块内部的数据不连续(例如,行主序矩阵中的列访问),缓存效率仍然会受损。数据打包 (Packing) 通过将需要计算的矩阵块复制到临时的、内存连续且对齐的缓冲区中来解决这个问题。
- 将 $ A $ 的 $ M_r \times K_c $ 面板按“列优先、行紧凑”的形式打包,便于微内核顺序读取。
- 将 $ B $ 的 $ K_c \times N_r $ 面板按“行优先、列紧凑”的形式打包,使得每个 $ k $ 的 $ B[k, j..j+N_r-1] $ 连续、对齐。
示例打包代码(以 $ M_r=4, N_r=4 $ 为例):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| // pack A: 从行主序 A 中取 4xKc,按列(k)主序、行(r)紧凑存放:Apack[k*4 + r]
void pack_A_4xKc(const float* A, int lda, float* Apack, int Kc) {
for (int k = 0; k < Kc; ++k) {
Apack[k * 4 + 0] = A[0 * lda + k];
Apack[k * 4 + 1] = A[1 * lda + k];
Apack[k * 4 + 2] = A[2 * lda + k];
Apack[k * 4 + 3] = A[3 * lda + k];
}
}
// pack B: 从行主序 B 中取 Kc x 4,按行(k)主序、列(c)紧凑存放:Bpack[k*4 + c]
void pack_B_Kc4(const float* B, int ldb, float* Bpack, int Kc) {
for (int k = 0; k < Kc; ++k) {
const float* bk = B + k * ldb;
Bpack[k * 4 + 0] = bk[0];
Bpack[k * 4 + 1] = bk[1];
Bpack[k * 4 + 2] = bk[2];
Bpack[k * 4 + 3] = bk[3];
}
}
|
配合打包的 4×4 微内核(内层线性访问):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| inline void AddDot4x4_packed(int Kc, const float* Ap, const float* Bp, float* Cij, int N) {
__m128 c0 = _mm_setzero_ps();
__m128 c1 = _mm_setzero_ps();
__m128 c2 = _mm_setzero_ps();
__m128 c3 = _mm_setzero_ps();
for (int k = 0; k < Kc; ++k) {
__m128 b = _mm_loadu_ps(&Bp[k * 4]);
float a0 = Ap[k * 4 + 0];
float a1 = Ap[k * 4 + 1];
float a2 = Ap[k * 4 + 2];
float a3 = Ap[k * 4 + 3];
c0 = _mm_add_ps(c0, _mm_mul_ps(_mm_set1_ps(a0), b));
c1 = _mm_add_ps(c1, _mm_mul_ps(_mm_set1_ps(a1), b));
c2 = _mm_add_ps(c2, _mm_mul_ps(_mm_set1_ps(a2), b));
c3 = _mm_add_ps(c3, _mm_mul_ps(_mm_set1_ps(a3), b));
}
_mm_storeu_ps(&Cij[0 * N], _mm_add_ps(c0, _mm_loadu_ps(&Cij[0 * N])));
_mm_storeu_ps(&Cij[1 * N], _mm_add_ps(c1, _mm_loadu_ps(&Cij[1 * N])));
_mm_storeu_ps(&Cij[2 * N], _mm_add_ps(c2, _mm_loadu_ps(&Cij[2 * N])));
_mm_storeu_ps(&Cij[3 * N], _mm_add_ps(c3, _mm_loadu_ps(&Cij[3 * N])));
}
|
- FLOPs:不变。
- DRAM 访存:与“理想分块”一致($ M K + K N + 2 M N $),但常数项更小(线性、对齐、可预取),SIMD 装载更高效。
OpenMP Parallelization#
在多核 CPU 上,使用 OpenMP 对外层块循环并行是提升性能的有效手段。推荐在线程之间划分 $ (i, j) $ 的宏块,避免对同一 $ C $ 子块的写冲突。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| // OpenMP 并行的分块 GEMM(以 4x4 微内核 + K 分块为例)
void gemm_blocked_omp(int M, int N, int K, const float* A, const float* B, float* C, int num_threads) {
const int MR = 4, NR = 4, KC = 256, MC = 256, NC = 256;
#pragma omp parallel num_threads(num_threads)
{
// 线程私有的临时打包缓冲区
std::vector<float> Ap(MR * KC), Bp(KC * NR);
#pragma omp for collapse(2) schedule(static)
for (int jc = 0; jc < N; jc += NC) {
for (int ic = 0; ic < M; ic += MC) {
int Nc = std::min(NC, N - jc);
int Mc = std::min(MC, M - ic);
for (int pc = 0; pc < K; pc += KC) {
int Kc = std::min(KC, K - pc);
for (int i = ic; i < ic + Mc; i += MR) {
int Mb = std::min(MR, ic + Mc - i);
for (int j = jc; j < jc + Nc; j += NR) {
int Nb = std::min(NR, jc + Nc - j);
if (Mb == MR && Nb == NR) {
pack_A_4xKc(&A[i * K + pc], K, Ap.data(), Kc);
pack_B_Kc4(&B[pc * N + j], N, Bp.data(), Kc);
AddDot4x4_packed(Kc, Ap.data(), Bp.data(), &C[i * N + j], N);
} else {
for (int ii = 0; ii < Mb; ++ii)
for (int jj = 0; jj < Nb; ++jj) {
float acc = 0.f;
for (int k = 0; k < Kc; ++k)
acc += A[(i + ii) * K + (pc + k)] * B[(pc + k) * N + (j + jj)];
C[(i + ii) * N + (j + jj)] += acc;
}
}
}
}
}
}
}
}
}
|
分析:
- FLOPs:不变。
- DRAM 访存:与“分块 + 打包”的单线程相同($ M K + K N + 2 M N $)。
- 加速上界:
- 计算主导:理想线性加速 $ \leq T $(线程数)。
- 内存主导:受内存带宽限制,$ \leq \frac{\text{BW}_{\text{并行}}}{\text{BW}_{\text{单线程}}} $。当达到带宽饱和后继续加线程收益有限。
加速比:
- 在“分块 + 打包”基础上,OpenMP 将计算并行化。理想上界(计算主导):$$
S_{\text{blocked+packed+OMP}} \approx \min\left(T,\ \frac{\text{PeakFLOPs}}{\text{单线程 FLOPs}}\right) \times \frac{4 M N K + M N}{M K + K N + 2 M N}
$$
- 在带宽主导时,上式中 $ T $ 替换为带宽扩展比。
Method Comparison#
为便于对比,下面给出各优化策略在“忽略缓存命中、以元素访问计”的内存访问与内存主导模型下的理论加速比(相对 naive):
| 方法 | 微内核形状 | FLOPs | 内存访问(元素数) | 相对 naive 加速比(内存主导,$ K \gg 1 $) |
|---|
| naive | 无 | $ 2MNK $ | $ 4MNK + MN $ | $ 1.0 $ |
| 1×4 寄存器分块 | 1×4 | $ 2MNK $ | $ 1.25MNK + MN $ | $ \approx 3.2 $ |
| 1×4 + 展开 | 1×4 | $ 2MNK $ | $ 1.25MNK + MN $ | $ \approx 3.2 $(计算主导再 +5%~15%) |
| 4×4 寄存器分块 | 4×4 | $ 2MNK $ | $ 0.5MNK + MN $ | $ \approx 8.0 $ |
| 4×4 + SIMD(SSE) | 4×4 | $ 2MNK $ | $ 0.5MNK + MN $ | 内存主导 $ \approx 8.0 $;计算主导再 $ \times 4 $ |
| 分块($ K_{c} $)+ 打包 | 任意 | $ 2MNK $ | $ MK + KN + 2MN $ | $ \frac{4MNK+MN}{MK+KN+2MN} $(方阵约为 $ n $) |
| 分块 + 打包 +OpenMP | 任意 | $ 2MNK $ | $ MK + KN + 2MN $ | 上式 × 并行效率(受带宽与可伸缩性限制) |
Comparing with BLAS Libraries#
- 现代 BLAS(如 Intel MKL、OpenBLAS、BLIS)普遍采用“三级分块 + 数据打包 + 专用微内核(含 SIMD/FMA)”的体系:
- 最外层:$ N_c $、$ M_c $、$ K_c $ 级别的宏分块,匹配 L3/L2。
- 中层:面板打包(AB-panel),顺序、对齐、预取友好。
- 内层:手写/内联汇编微内核,固定 $ M_r \times N_r $,深度展开,寄存器阻塞,利用 FMA 与流水线。
- 对 x86:
- SSE 场景常见微内核大小约 $ 4 \times 4 $。
- AVX2/AVX-512 场景常见 $ M_r, N_r $ 更大(如 $ 6 \times 16 $、$ 8 \times 30 $ 等),并利用 FMA。
- 这些库还会进行:
- 多级预取策略(硬件/软件结合)。
- NUMA 感知的任务分配与内存归属(first-touch)。
- 针对边界块的专门路径和对齐优化。
Summary#
References#

