EmT | diefish's blog

Abstract

问题：现有 EEG 情绪识别方法对长期上下文信息关注不足，导致跨被试泛化能力减弱
方案：提出 Emotion Transformer (EmT) ，为 Graph-Transformer 混和架构
核心模块：
1. TGC：将 EEG 信号转换为时序图序列
2. RMPG：使用残差多视图金字塔 GCN，学习动态、多尺度的空间连接模式，生成 token（核心）
3. TCT：使用任务自适应的 Transformer，学习 token 序列上下文（核心）
4. TSO：输出分类/回归结果
成果：在多个公开数据集的广义跨被试任务上面超过了 baseline

为什么 EEG 难以使用跨被试 (cross-subject) 的场景？

个体差异：不同被试生理结构和认知策略差异，导致 EEG 模式不同
低信噪比：EEG 信号容易受到外源噪声干扰（肌电、眼电……）

目标是学习一种跨被试共享、具有泛化能力的情绪表征

Gpaph Neural Networks

核心思想：EEG 数据具有非欧图结构，适合使用 GNN 来处理
代表工作：
- ChebyNet：使用切比雪夫多项式近似光谱滤波，EmT 模型中采用其作为 GCN 层
- GCN：通过局部一阶聚合近似光谱滤波
- DGCNN / RGNN：使用 GNNs 提取 EEG 空间信息；依赖单一的邻接矩阵，忽略时序上下文，具有局限性；而 EmT 通过多视图可学习邻接矩阵和时序图来弥补

Temporal Context Learning

核心理念：情绪是连续认知过程，EEG 信号中嵌入时序上下文信息
代表工作：
- LSTM / TCN / TESANet / Conformer / AMDET
- 局限性：这些方法通常从扁平化的 EEG 特征向量学习，可能未能有效学习空间关系；EmT 则通过并行 GCN 和 STA 层更有效地捕捉时空信息

EEG Emotion Recognition

核心理念：EEG 情绪识别面临个体差异大、信噪比低等挑战，需提取光谱、空间、时序特征
代表工作：
- GCB-Net / TSception
- 局限性：没有关注长时序上下文信息

Method

EmT 是一个端到端的框架，包含四大模块：

raw EEG -> TGC -> 时序图 -> RMPG -> Tokens -> TCT -> 深层特征 -> TSO -> Result

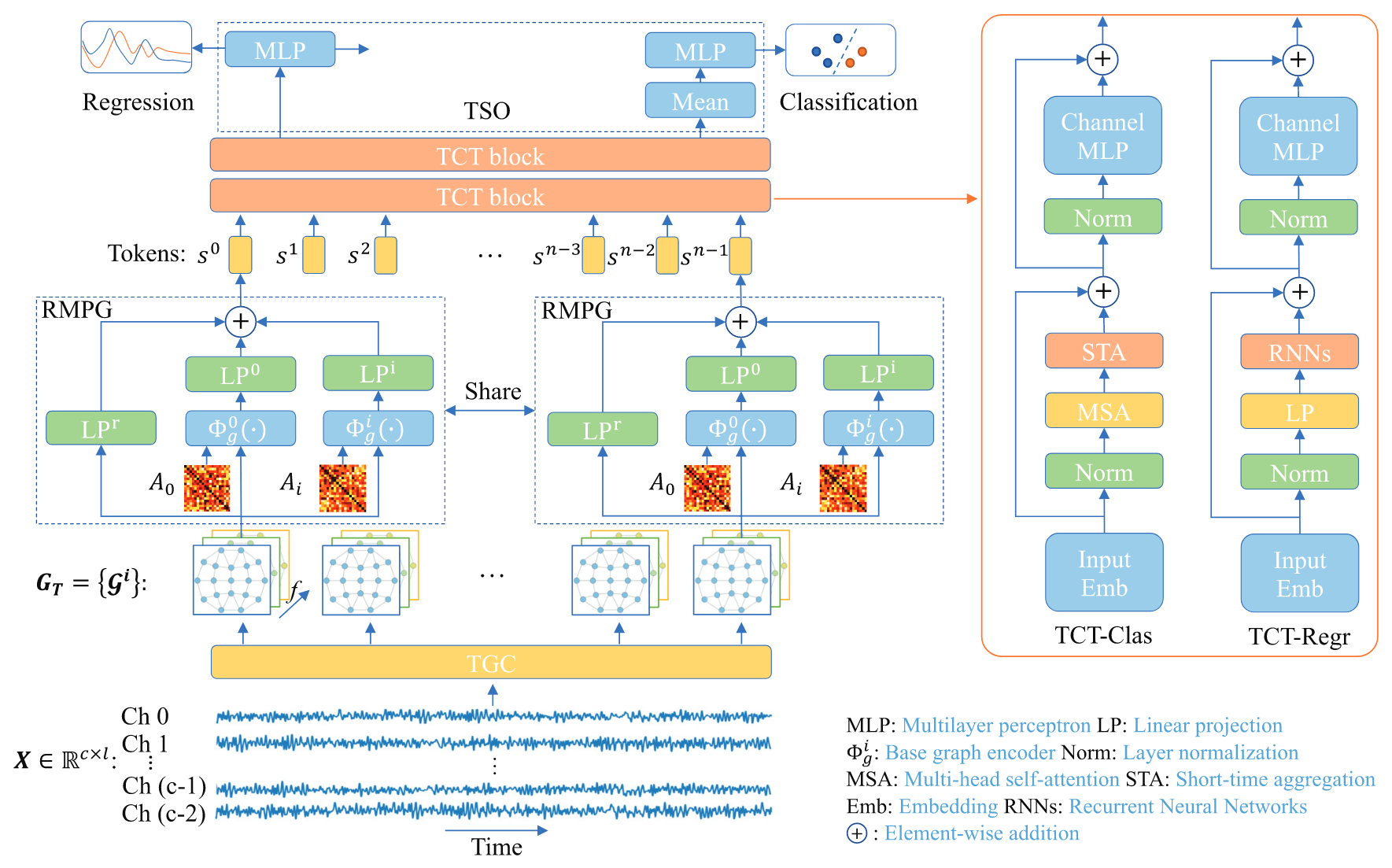
EEG-Temporal-Graph Representations (TGC)

目标：将连续的 EEG 信号转化为结构化的时序图序列

图：每个“图”是指在一个短的窗口内大脑状态的数学表示，图中的每个节点对应一个 EEG 电极通道，节点的特征是该通道在 7 个不同的频段上的 rPSD
时序序列：序列是通过滑动窗口技术截取的一段较长的 EEG 数据里面切分成许多重叠的短的子片段，每个子片段生成的图所形成的序列

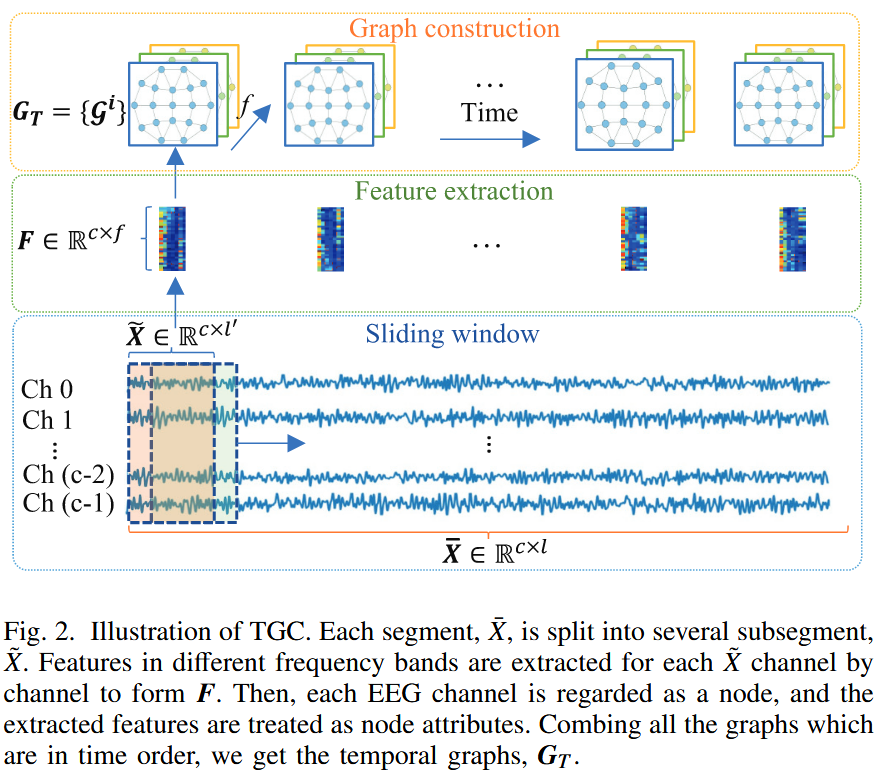
双层滑动窗口分段：为了捕捉不同时间尺度上的信息，TGC 采用了一种双层分段策略
- 首先将一次完整实验的 (trail) 的 EEG 数据，表示为 $ X \in \mathbb{R}^{c \times L} $ （其中 $ c $ 为通道数，$ L $ 为总采样点数），通过一个较长的滑动窗口（长度为 $ l $ ，步长为 $ s $ ）分割成多个重叠的长片段 $ \overline{X} \in \mathbb{R}^{c \times l} $
- 接着对于每一个长片段 $ \overline{X} $ 使用一个更短的滑动窗口（长度为 $ l' $ ，步长为 $ s' $ ）将其分割为一系列子片段 $ \tilde{X} \in \mathbb{R}^{c \times l'} $
- 这使得模型能够在一个长片段的标签下，观察到内部更精细的信号动态变化，为后续的 Transformer 模块捕捉时间上下文提供了基础
节点特征提取：对于每一个子片段 $ \tilde{X} $，需要为其对应的图节点（即 EEG 通道）提取有意义的特征，论文选择了相对功率谱密度 (Relative PSD, rPSD) 作为节点属性
- 具体地，使用 welch’s method 计算每个 EEG 通道在七个经典频带上的 rPSD
- 这样，每个子片段 $ \tilde{X} $ 都对应一个特征矩阵 $ F \in \mathbb{R}^{c \times f} $，其中 $ f=7 $

最终，一个长片段 $ \overline{X} $ 被转换成一个按时间顺序排列的图序列 $ G_{T} = \{\mathcal{G}^{i}\} \in \mathbb{R}^{seq \times c \times f} $，其中 $ seq $ 是子片段的数量。这个时间图序列就是 RMPG 模块的输入

Residual Multiview Pyramid GCN (RMPG)

核心：解决传统 GNN“单一视角”问题，为时间图序列 $ G_{T} $ 中的每一个图 $ \mathcal{G}^i $ 学习一个丰富的、多层次的空间表征，并将其压缩成一个单一的 token ，以供后续的 TCT 模块处理

RMPG 模块由一个基础的图编码器 $ \Phi_{g}(\cdot) $ 构成，文中采用了 ChebyNet 作为基础图编码器，对于给定特征输入 $ F^{m-1} $ 和邻接矩阵 $ A $ （通过拉普拉斯算子 $ \hat{L} $ 转换） $$ \Phi_{g}(F^{m}, A) = \sigma\left( \sum_{k=0}^{K-1}\theta_{k}^{m}T_{k}(\hat{L})F^{m-1} - b^{m}\right) $$ 其中 $ m $ 为 GCN 层的索引，$ \sigma $ 为 ReLU 激活函数，$ \theta $ 为参数，$ T_{k} $ 为 $ k $ 阶 Chebyshev 多项式

多视图学习 (Multiview Learning) ：为了模拟情绪背后多种认知子过程驱动的不同大脑连接模式，RMPG 并非使用单一的图卷积网络，而是并行地使用了多个 GCN 分支，$ \{ \Phi_{g}^{0}(\cdot), \Phi_{g}^{1}(\cdot), \dots, \Phi_{g}^{i}(\cdot) \} $
- 每个分支都拥有一个独立的可学习邻接矩阵 $ A^{i} \in \mathbb{R}^{c \times c} $ ，能在模型训练过程中通过梯度反向传播进行端到端的优化
- 这意味着每个 GCN 分支都能从数据中学习到一种独特的大脑功能连接“视图”
金字塔学习 (Pyramid Learning) ：为了捕捉不同尺度的空间信息，并行的 GCN 分支被设计成具有不同的深度（即 GCN 层数）
- 较浅的 GCN 能够有效地聚合全局的、跨脑区的功能连接信息，聚合远距离节点的信息而不过度平滑
- 较深的 GCN 能够更好地聚合局部邻域内的信息，在脑区内部形成一致的表征
- GCN 的深度越深，其输出所代表的特征金字塔层级越高。
残差连接 (Residual) ：除了并行的 GCN 分支外，RMPG 还包含一个并行的线性残差分支。该分支直接对原始的时序图 $ G $ （或者对应的特征矩阵 $ F $ ）进行线性投影，不经过任何图卷积，从而保留最原始的节点信息，作为特征金字塔的“基座”
- 线性投影层 $ LP(\cdot) $ 将扁平化的图表示投影到隐藏嵌入 $ H_{g}^{i} \in \mathbb{R}^{d_{g}} $
- 堆叠来自不同层的 GCN 的并行输出，得到多金字塔视图嵌入 $$ \{ H_{g}^{i} \} = \{ LP^{i}(\Gamma(\Phi_{g}^{i}(F, A^{i}))) \} $$ 其中 $ \Gamma(\cdot) $ 是扁平操作，$ \{ \cdot \} $ 是堆叠操作

特征融合与 Token 生成：最终，对于图序列中的每一个图 $ G_{i} $，其所有 GCN 视图的输出 $ \{ H_{i}^{g} \} $ 和残差基座 $ H_{g-\text{base}} $ 通过一个 mean fusion 操作合并成当前时间步 $ i $ 的最终 token $ s_{i} $ $$ s_{i} = \text{mean}(\{ H_{g-\text{base}}, H_{g}^{0}, H_{g}^{1}, \dots, H_{g}^{i} \}) $$

通过 RMPG 模块，输入的图序列 $ G_{T} $ 被高效地转化为一个 token 序列 $ S_{T}=\{ s^{i} \} \in \mathbb{R}^{seq \times d_{g}} $ ，这个序列既蕴含了每个时刻丰富的多视图、多层次空间信息，又具备了适合 Transformer 处理的格式

Temporal Contextual Transformer (TCT)

核心：接受由 RMPG 生成的 token 序列 $ S_{T} $ ，并利用 Transformer 的结构来高效捕捉这些 token 之间的时间依赖关系；与标准的 Transformer 不同，TCT 引入了两种为 EEG 情绪识别任务定制的 Token Mixer，分别用于分类和回归任务

TCT 模块由多个堆叠的 Transformer Block 组成，对于输入 token 序列 $ Z^{m} $ （ $ Z^{0} = S_{T} $ ），每个 Block 的计算过程为 $$ Z^{m'} = \text{TokenMixer}(\text{Norm}(Z^{m})) + Z^{m} $$ $$ Z^{m+1} = \text{MLP}(\text{Norm}(Z^{m'})) + Z^{m'} $$ 其中 $ m $ 是层的索引，MLP 是带 ReLU 激活函数的两层感知机

$ \text{TokenMixer}_{\text{clas}} $ for Classification Tasks

旨在捕捉随时间变化的长短时序上下文信息

多头自注意力 (Multi-head Self-Attention, MSA) ：用于全局地关注序列中与整体情绪状态高度相关的部分 $$ \text{Attn}(Q,K,V) = \text{softmax}\left( \frac{QK^{T}}{\sqrt{ d }} \right)V $$
- 并行应用多个注意力头（每个头有独立的 $ LP_h(\cdot) $ 来生成 $ Q, K, V $），然后将所有头的输出拼接：$$ \text{MSA}(S_{T}) = \text{Concat}(\text{Attn}(LP_0(S_{T})), ..., \text{Attn}(LP_{n_{\text{head}}-1}(S_{T}))) $$ 其中 $ S_{T} $ 是 token 序列，$ n_{\text{head}} $ 是注意力头的数量
短期聚合层 (Short-Time Aggregation, STA) ：
- 基于“情绪短期连续而长期变化”的先验知识，STA 在 MSA 之后应用来学习短期的上下文信息
  - 首先对 MSA 的输出 $ H_{\text{attn}} \in \mathbb{R}^{n_{\text{head}} \times \text{seq} \times d_{\text{head}}} $ 应用一个带有比例因子 $ \alpha $ 的 Dropout 层 $ \text{dp}(\alpha) $
  - 接着，通过 Conv2D 聚合 $ n_{\text{anchor}} $ 个时序近邻
  - Conv2D 的卷积核 $ K_{\text{cnn}} $ 的尺寸为 $ (n_{\text{anchor}}, 1) $，步长为 $ (1,1) $
  - 最后，卷积的输出会被 Reshape 并进行线性投影（$ W_{\text{sta}} $）
  - 可以描述为 $$ \text{STA}(H_{\text{attn}}) = \text{Reshape}(\text{Conv2D}(\text{dp}(H_{\text{attn}}), K_{\text{cnn}})) W_{\text{sta}} $$ $ \text{Reshape}(\cdot) $ 将维度从 $ (n_{\text{head}},\text{seq},d_{\text{head}}) $ 转换为 $ (\text{seq}, n_{\text{head}} \cdot d_{\text{head}}) $ ， $ W_{\text{sta}} \in \mathbb{R}^{n_{\text{head}} \cdot d_{\text{head}} \times d_g} $ 是投影权重矩阵
$ \text{TokenMixer}_{\text{Clas}} $ 最终由上述两个模块串联构成 $$ \text{TokenMixer}_{\text{clas}}(S_{T}) = \text{STA}(\text{MSA}(S_{T})) $$

$ \text{TokenMixer}_{\text{regr}} $ for Regression Tasks

旨在预测序列中情绪状态的连续变化

不同于分类任务：分类任务的目标通常是从整个序列中提取几个核心特征来判断整体情绪状态，这通过 MSA 聚焦于重要部分是有效的；然而回归任务需要模型对序列中每个时步的连续情绪变化进行预测，因此不使用全局的 MSA，而是采用了一种基于 RNN 的混合器（ RNN family ）
RNN Mixer ：
- RNN 结构天然适合处理连续序列的演变过程，能够更好地建模情绪值的平滑变化
- 经验性选择的两层双向 GRU (bi-directional GRU) 作为 $ \text{TokenMixer}_{\text{regr}} $ ，输出长度为 $ 2 \times d_{\text{head}} $
计算过程为 $$ \text{TokenMixer}_{\text{regr}}(S_T) = \text{RNNs}(\text{LP}(S_T)) $$ 其中 $ LP(S_{T}) = S_{T}W_{v} $ ，把 token 序列投影为 $ V $ 值

TSO Module

头部接收来自不同 Token Mixer 的输出：用于分类的 $ S_{\text{clas}} $ 和用于回归的 $ S_{\text{regr}} $

分类任务：对所有 token 进行 mean fusion ，再通过线性层得到最终 logits $$ \hat{Y}_{\text{clas}} = \text{mean}(S_{\text{clas}})W_{\text{clas}} + b_{\text{clas}} $$ 其中 $ S_{\text{clas}} \in \mathbb{R}^{\text{seq} \times d_{\text{head}}} $ ，$ W_{\text{clas}} \in \mathbb{R}^{d_{\text{head}} \times d_{\text{class}}} $ ，$ b_{\text{clas}} \in \mathbb{R}^{n_{\text{class}}} $
回归任务：直接将每个时间步的 token 特征通过线性层，得到对应每个时刻的回归值 $$ \hat{Y}_{\text{regr}} = S_{\text{regr}}W_{\text{regr}} + b_{\text{regr}} $$ 其中 $ S_{\text{regr}} \in \mathbb{R}^{\text{seq} \times 2\cdot d_{\text{head}}} $ （双向），$ W_{\text{regr}} \in \mathbb{R}^{2\cdot d_{\text{head}} \times 1} $ ，$ b_{\text{regr}} \in \mathbb{R} $

Experiment

Datasets

使用 SEED, THU-EP, FACED, MAHNOB-HCI 四个公开数据集

其中 SEED 数据集使用了 0.3-50 Hz 的带通滤波

EEG-Temporal-Graph

长片段：窗口长度 $ l=20\,\mathrm{s} $ （即 $ 20 \times f_{s} $ ），步长 $ s=4\,\mathrm{s} $
子片段：
- 对于 SEED 和 THU-EP： $ l'=2\,\mathrm{s},s'=0.5\,\mathrm{s} $
- 对于 FACED： $ l'=4\,\mathrm{s},s'=1\,\mathrm{s} $

Settings

数据划分：
- SEED：采用留一被试交叉验证，每次迭代一个被试的数据作为测试集，剩余数据中 80% 作为训练集，20% 作为验证集
- THU-EP 和 FACED：采用留 $ n $ 被试交叉验证，其中 $ n_{\text{THU-EP}}=8,n_{\text{FACED}}=12 $ ，训练数据中 10% 作为验证集
分类任务：对 SEED、THU-EP 和 FACED 进行积极/消极情绪的二分类，THU-EP 和 FACED 的效价分数通过阈值 3.0 划分为高/低效价
回归任务：MAHNOB-HCI 并进行 LOSO 验证

Evaluation Metrics

Classfication

Accuracy：$$ \text{Accuracy} = \frac{\text{TP + TN}}{\text{TP + FP + TN + FN}} $$
F1 Score：$$ \text{F1} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision + Recall}} = \frac{\text{TP}}{\text{TP} + \frac{1}{2}(\text{FP} + \text{FN})} $$

其中 $ \text{TP} $ 表示真阳性，$ \text{TN} $ 表示真阴性，$ \text{FP} $ 表示假阳性，$ \text{FN} $ 表示假阴性

Regression

给定预测值 $ \hat{y} $ 和连续标签 $ y $ ：

均方根误差 (RMSE) ：$$ \text{RMSE} = \sqrt{\frac{1}{N} \sum_{i=0}^{N-1} (\hat{y}_i - y_i)^2} $$
皮尔逊相关系数 (PCC) ：$$ \text{PCC} = \frac{\sigma_{\hat{y}y}}{\sigma_{\hat{y}} \sigma_y} = \frac{\sum_{i=0}^{N-1} (\hat{y}_i - \mu_{\hat{y}})(\hat{y}_i - \mu_y)}{\sqrt{\sum_{i=0}^{N-1} (\hat{y}_i - \mu_{\hat{y}})^2} \sqrt{\sum_{i=0}^{N-1} (y_i - \mu_y)^2}} $$
一致性相关系数 (CCC) ：$$ \text{CCC} = \frac{2\sigma_{\hat{y}y}}{\sigma^2_{\hat{y}} + \sigma^2_y + (\mu_{\hat{y}} - \mu_y)^2} $$

其中 $ N $ 是向量中的元素数量，$ \sigma_{\hat{y}y} $ 是协方差，$ \sigma_{\hat{y}} $ 和 $ \sigma_y $ 是标准差，$ \mu_{\hat{y}} $ 和 $ \mu_y $ 是均值

Implementation Details

模型的三种变体：

Analyses

Classification

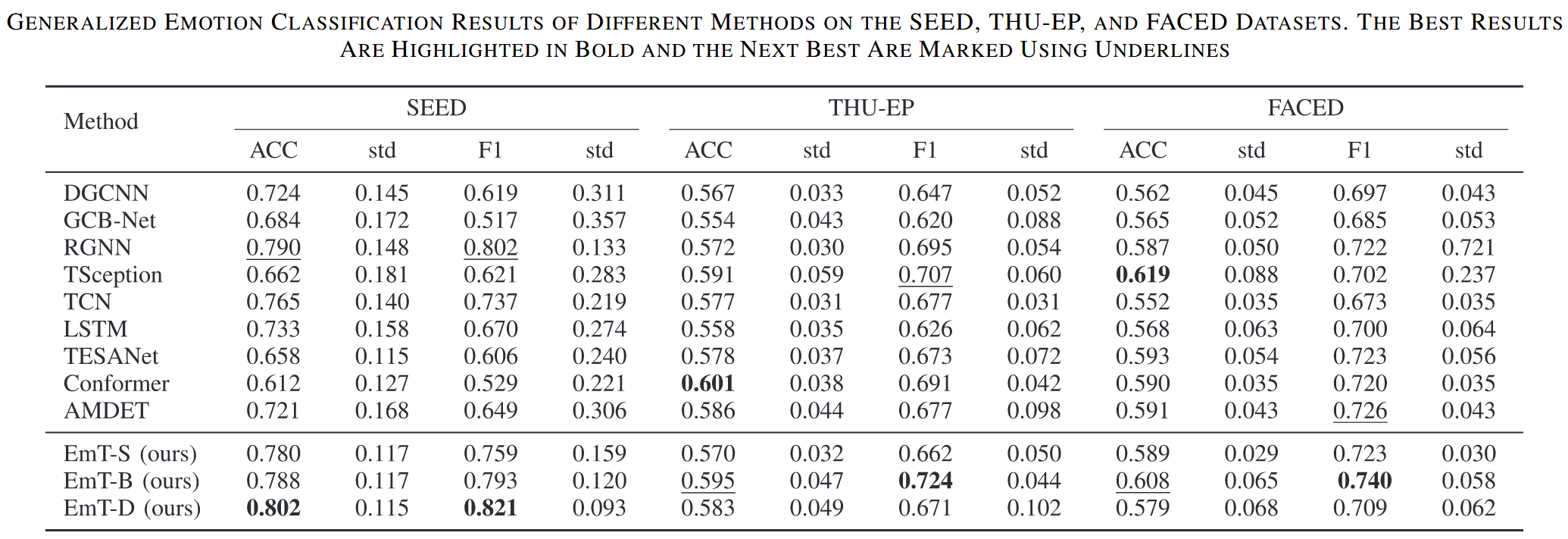
SEED：
- EmT-D 表现最佳，EmT-B 和 EmT-S 表现也良好，RGNN 表现第二佳
- 使用特征作为输入的模型通常优于直接使用 EEG 信号作为输入的模型，从时序特征而非直接特征学习通常能取得更好的性能（RGNN 除外），这表明了学习时序上下文信息的有效性，EmT 借助基于 GCN 的模块，能更好地学习空间信息
THU-EP / FACED：
- THU-EP：EmT-B 取得了最佳 F1 分数，Conformer 取得了最佳 ACC
- FACED：EmT-B 取得了第二佳 ACC 和最佳 F1 分数
- 由于类不平衡，F1 分数比 ACC 更重要，EmT-B 在这两个数据集上均取得了最高 F1 分数
- 与 SEED 不同，直接使用 EEG 作为输入的 baseline 模型表现更好，这可能因为这两个数据集的被试人数更多
Features：
- SEED (62 channels，15 subjects) ：EmT-D (8 层) 表现最佳，说明 Transformer 层数越多，学到的空间信息越丰富
- THU-EP 和 FACED (32 channels，more subjects) ：EmT-B (4 层) 表现更好，通道数少且被试间变异性大时，更深的模型（EmT-D）容易过拟合

Regression

在 MAHNOB-HCI 数据集上，EmT-Regr (LP+LSTM) 取得了最低的 RMSE，而 EmT-Regr (LP+GRU) 取得了最佳的 PCC 和 CCC
使用 MSA 作为 Token Mixer 时，模型性能急剧下降，甚至低于所有基线模型
这表明对于回归任务，融合所有片段的信息至关重要，而 RNN 的顺序信息融合能力比 MSA 更适合建模连续的情绪变化

Ablation Study

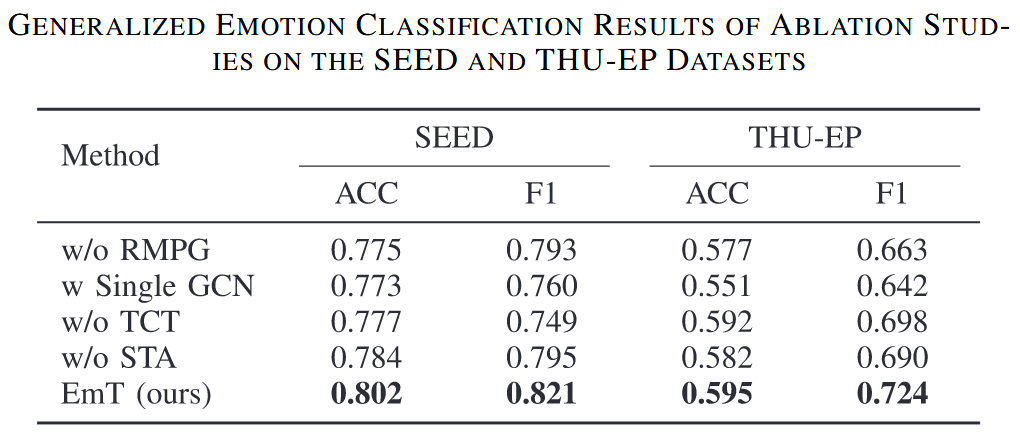
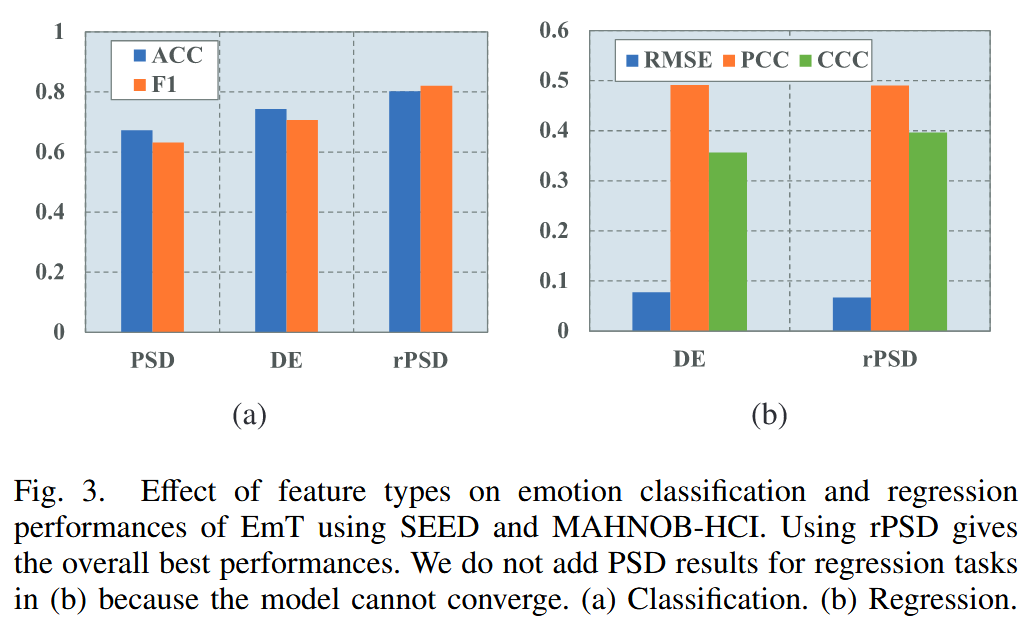
Effect of EEG Features

Effect of The Depth and Width of GCNs in RMPG

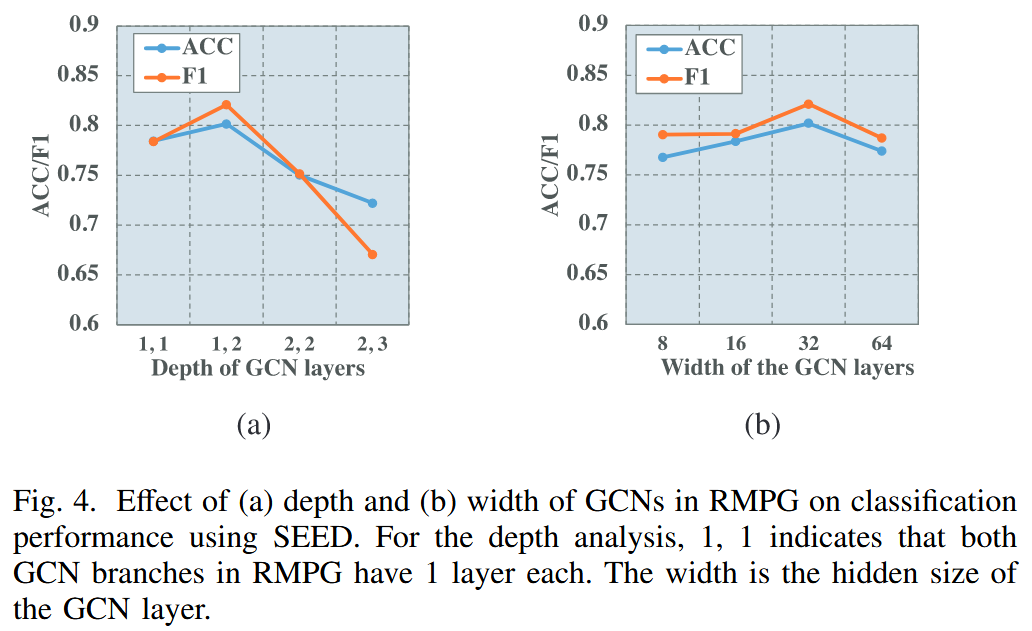
Depth：增加 GCN 层的数量会导致性能显著下降，这与更深 GCN 中存在的过平滑问题一致
Width：宽度从 8 增加到 32 时，性能呈正相关；当宽度进一步增加时，性能下降，这可能是由更大的模型尺寸导致的过拟合

Effect of The Number of TCT Blocks

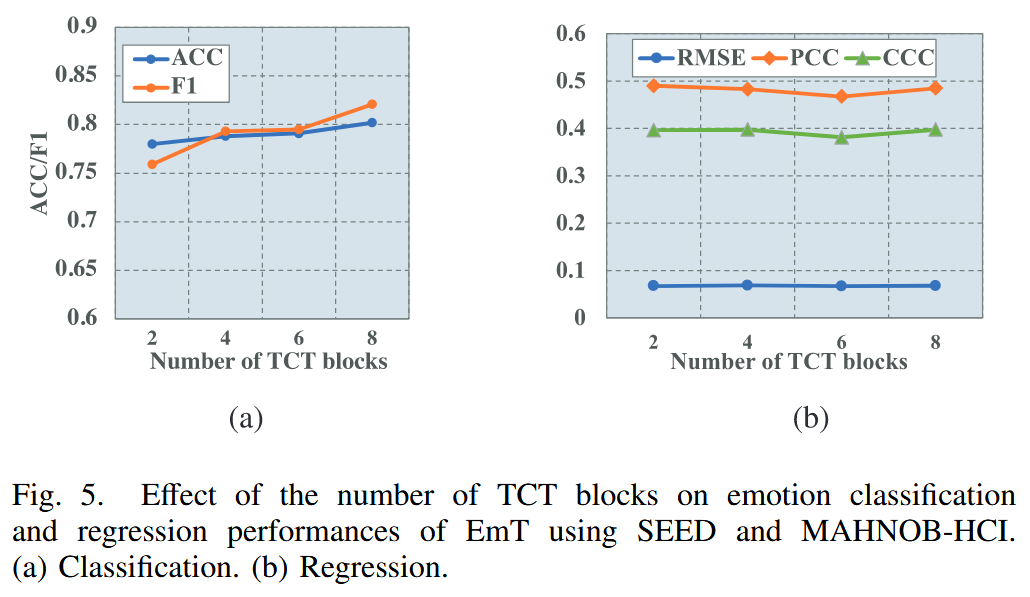
Classfication (SEED) ：TCT 块的数量从 2 增加到 8 时，ACC 和 F1 分数均显著提高，这表明增加 TCT 块数能增强模型捕捉时序上下文信息的能力，从而提升分类性能
Regression (MAHNOB-HCI) ：TCT 块的数量对性能指标几乎没有影响

Visualization

Learned Connections

在 SEED 数据集上学习到的两种不同连接模式的可视化证据

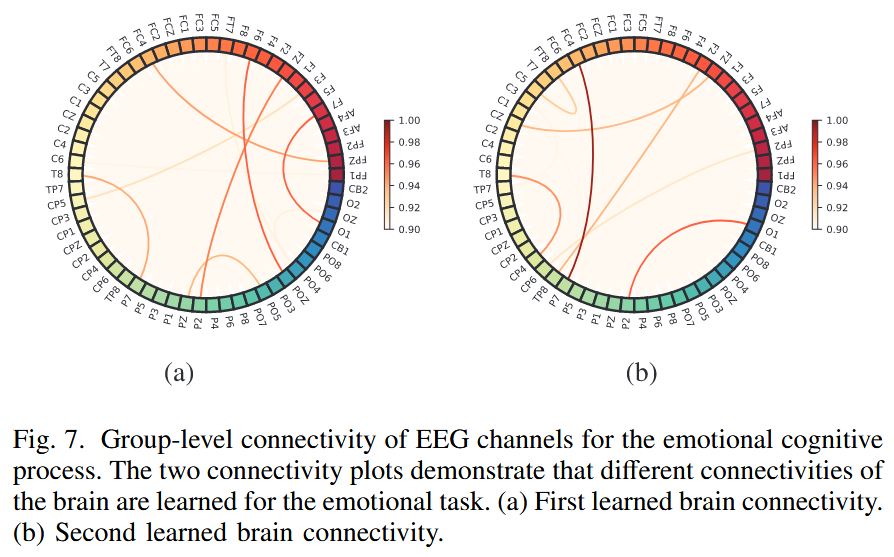
在 SEED 数据集上，两个可学习的邻接矩阵揭示了情绪认知过程中不同的连接模式：

(a) 中主要关注额叶、顶叶和颞叶区域之间的连接，这些区域与心理注意力密切相关
(b) 中则包括额叶、颞叶和顶叶区域之间的互动（与情绪相关），以及枕叶和顶叶区域的互动（与视觉过程相关，因为刺激为视频）

Learned Temporal Contextual Information

Classfication (FACED)

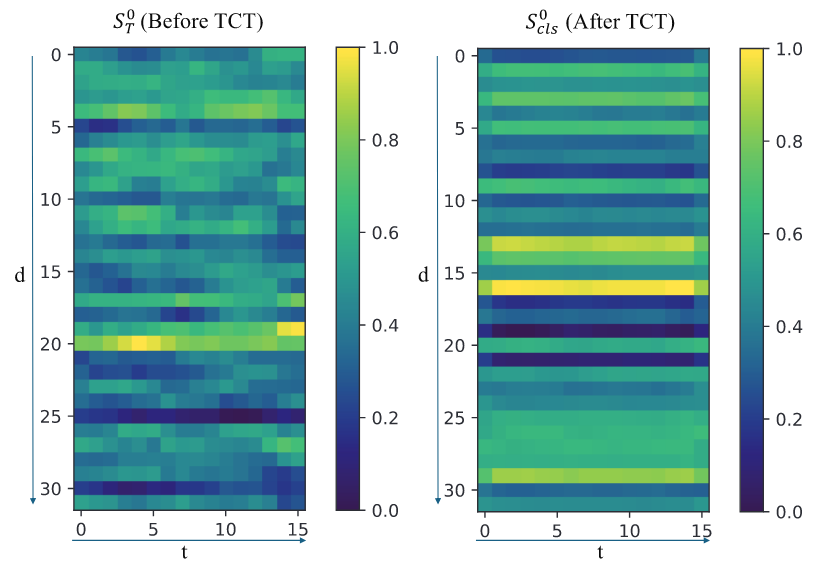
Regression

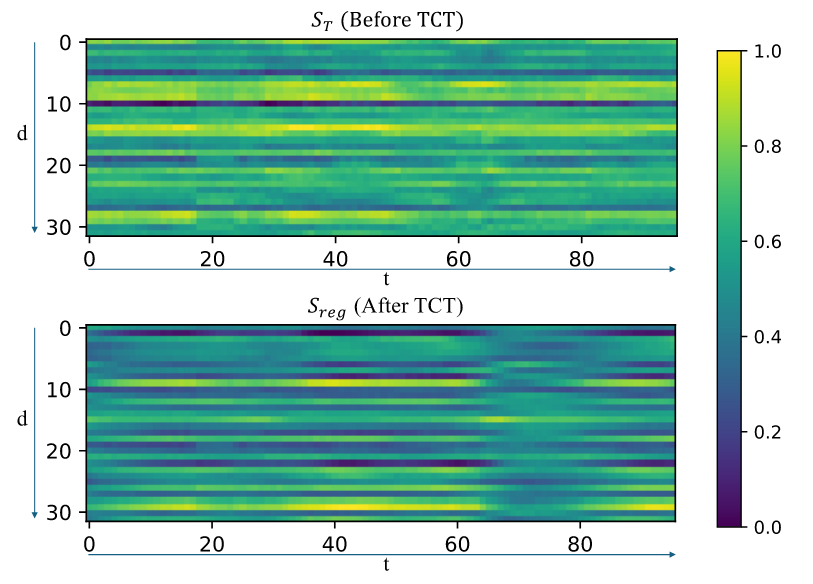
分类任务在 TCT 块之前，特征随时间变化，TCT 块之后，激活变得更加一致；这可能是因为自注意力机制关注与整体情绪状态高度相关的部分，而 STA 层通过聚合邻近的时序信息来平滑波动
回归任务：特征空间也显示出时序变化；与分类不同，回归特征并非简单平滑，形成了更复杂的表示
总结：TCT 块处理分类和回归任务的方式不同：分类中，特征被平滑以增强可分离性；回归中，RNN Token Mixer 保留了时序变化，从而实现连续情绪预测

Abstract#

Introduction & Related Work#

Gpaph Neural Networks#

Temporal Context Learning#

EEG Emotion Recognition#

Method#

EEG-Temporal-Graph Representations (TGC)#

Residual Multiview Pyramid GCN (RMPG)#

Temporal Contextual Transformer (TCT)#

$ \text{TokenMixer}_{\text{clas}} $ for Classification Tasks#

$ \text{TokenMixer}_{\text{regr}} $ for Regression Tasks#

TSO Module#

Experiment#

Datasets#

EEG-Temporal-Graph#

Settings#

Evaluation Metrics#

Classfication#

Regression#

Implementation Details#

Analyses#

Classification#

Regression#

Ablation Study#

Effect of EEG Features#

Effect of The Depth and Width of GCNs in RMPG#

Effect of The Number of TCT Blocks#

Visualization#

Learned Connections#

Learned Temporal Contextual Information#

Abstract

Introduction & Related Work

Gpaph Neural Networks

Temporal Context Learning

EEG Emotion Recognition

Method

EEG-Temporal-Graph Representations (TGC)

Residual Multiview Pyramid GCN (RMPG)

Temporal Contextual Transformer (TCT)

$ \text{TokenMixer}_{\text{clas}} $ for Classification Tasks

$ \text{TokenMixer}_{\text{regr}} $ for Regression Tasks

TSO Module

Experiment

Datasets

EEG-Temporal-Graph

Settings

Evaluation Metrics

Classfication

Regression

Implementation Details

Analyses

Classification

Regression

Ablation Study

Effect of EEG Features

Effect of The Depth and Width of GCNs in RMPG

Effect of The Number of TCT Blocks

Visualization

Learned Connections

Learned Temporal Contextual Information