Abstract
现有 TTA 方法在处理图数据时,对节点属性偏移有效,但是对图结构偏移(同质性、节点度的变化)效果很差。原因是结构偏移会严重破坏节点表示的质量,使不同类别的节点在特征空间中混在一起。为此论文提出了 Matcha 框架,通过在测试的时候自适应地调整 GNN 的“跳数聚合参数 (hop-aggregation parameters)”,并且引入了新的预测感知的聚类损失函数来表示恢复节点表示的质量,从而有效应对结构偏移,并能和现有 TTA 方法相结合,进一步提高性能。
Introduction
GNN 的脆弱性:GNNs 在各类图任务上的表现依赖于训练数据和测试数据分布相同的假设,然而在现实世界中,图的分布常常会发生变化(分布偏移),分为:
属性偏移 (Attribute Shift):节点的特征发生变化。例如不同社交平台,即使用户一样,其账号的内容也会因为平台差异而不同。
结构偏移 (Structure Shift):节点的连接方式发生变化。比如工作平台用户倾向于连接同事,生活平台用户倾向于连接家人朋友。这种连接模式的变化就是结构偏移,具体表现为同质性 (Homophily) 和 节点度 (Degree) 的变化。
TTA 的局限性:TTA 允许一个预训练好的模型在不访问原始训练数据的情况下,利用无标签的测试数据进行自适应调整 。目前 TTA 在计算机视觉领域处理图像损坏、风格变化等属性偏移问题上很成功 。然而为图像处理设计的 TTA 方法直接应用到图上时,其在处理图结构偏移时的性能提升非常有限,几乎失效。
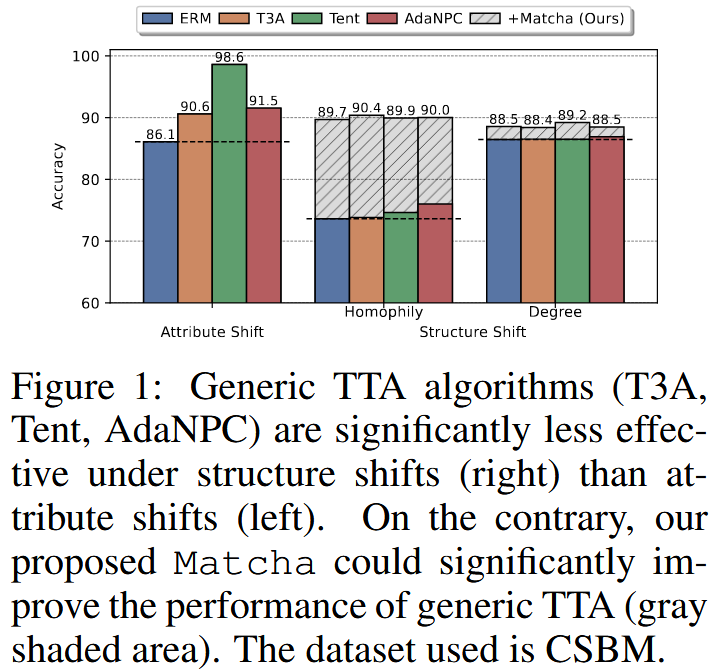
Analysis
两种偏移方式对 GNN 的影响存在本质不同。
Perliminaries
论文聚焦于 GTTA 任务。一个 GNN 模型可以被看成两个部分的组合,一个特征提取器 $ f_{S} $ ,一个分类器 $ g_{S} $ ,通常是一个线性层。
两种偏移的正式定义:
- 属性偏移:源图和目标图中,节点的条件概率分布不同 $ \mathbb{P}^{S}_{x | y} \neq \mathbb{P}^{T}_{x | y} $ 。
- 结构偏移:图的邻接矩阵和标签的联合分布不同,即 $ \mathbb{P}^{S}_{A \times Y} \neq \mathbb{P}^{T}_{A \times Y} $ 。论文主要关注两种具体的结构偏移:
- 度偏移:源图和目标图的平均节点度数不同。
- 同质性偏移:源图和目标图的同质性水平不同。其中图的所有节点同质性的平均值 $ h(\mathcal{G}) = \dfrac{1}{N}\sum_{i}h_{i} $ ,单个节点 $ v_{i} $ 的同质性计算公式为: $$ h_{i} = \dfrac{\left| \{ v_{j} \in \mathbb{N}(v_{i}): y_{j} = y_{i} \} \right|}{d_{i}} $$ 其中 $ y $ 表示节点标签,$ d $ 表示节点度数。
Impact of Distribution Shifts
通过数学建模来显示两种偏移的不同影响机制。
分析工具
CSBM (上下文随机块模型):广泛用于 GNN 分析的随机图生成器。参数 $ \mu_{+},\mu_{-} $ 编码节点属性,而 $ d,h $ 参数编码图的结构。
单层 GCN:为了简化分析,使用了一个单层的 GCN 模型,其节点表示 $ z_{i} $ 的计算公式为: $$ z_{i} = x_{i} + \gamma \cdot \dfrac{1}{d_{i}} \sum_{v_{j} \in \mathbb{N}(v_{i})}x_{j} $$ 其中 $ \gamma $ 是一个关键的跳数聚合参数,控制节点自身特征和邻居平均特征的混合比例。
推论 3.1
在 CSBM 图上,一个节点的最终表示 $ z_{i} $ 服从一个正态分布,其均值取决于节点的真实类别、图的同质性 $ h_{i} $ 以及 $ \gamma $ 参数,而方差取决于节点度数 $ d_{i} $ 和 $ \gamma $ 参数 $$ z_{i} \sim \mathcal{N}\left( (1 + \gamma h_{i})\mu_{+} + \gamma(1-h_{i})\mu_{-}, \left( 1 + \dfrac{\gamma^{2}}{d_{i}} \right)I \right) $$
推论 3.2
基于 3.1 直接给出了模型预期准确率的公式 $$ \text{Acc} = \varPhi\left( \sqrt{ \dfrac{d}{d+\gamma^{2}} } \cdot \left| 1 + \gamma(2h - 1) \right| \cdot \| \mu \|_{2} \right) $$ 根据这个公式,只需要输入图的度数,同质性和 $ \gamma $ 参数就能直接计算出模型的理论最高准确率,从而让定量分析成为可能。
准确率差距分解
论文指出当模型性能下降时,可能的原因有两种:
表示退化 $ \Delta_{f} $:GNN 的特征提取器出现了问题,其生成的节点表示本身质量就很差,无法区分不同类型的节点。
分类器偏移 $ \Delta_{g} $:指特征提取器本身没有问题,但是分类器出现了问题。
命题 3.3 (属性偏移的影响)
理论证明,在属性偏移下,性能损失完全来自于分类器偏移 $ \Delta_{g} $ ,而表示退化 $ \Delta_{f} $ 为零 。 $$ \Delta_{f} = 0, \Delta_{g} = \Theta (\| \Delta \mu \| _{2}^{2}) $$
这解释了为什么现有的 TTA 方法(主要调整分类器)在处理属性偏移时有效 。
命题 3.4 (结构偏移的影响)
理论证明,在结构偏移下,情况恰恰相反 。性能损失完全来自于表示退化 $ \Delta_{f} $,而分类器偏移 $ \Delta_{g} $ 为零 。 $$ \Delta_{f} = \Theta(\Delta h + \Delta g),\Delta_{g} = 0 $$
这是论文的核心发现,揭示了现有 TTA 方法在结构偏移下失效的根本原因:它们没有修复问题的根源——已经退化了的节点表示 。
命题 3.5 (调整跳聚数参数)
既然结构偏移的病根在于表示退化,那么治疗方案就必须调整特征提取器 。
论文证明调整跳数聚合参数 $ \gamma $ 是一个有效的方法,可以缓解表示退化问题 。
其关键在于,最优的 $ \gamma $ 值本身就依赖于图的度和同质性 $ \gamma_{T} = d_{T}(2h_{T} - 1) $。因此,通过在测试时将 $ \gamma $ 调整到适应目标图的新值,就可以提升模型的准确率 。这为后续 Matcha 框架的提出提供了理论基础。
Adapting Hop-Aggregation Parameters
根据前面的分析,解决结构偏移的影响关键在于调整特征提取器 $ f_{S} $ 来恢复节点表示的质量。
命题 3.5 (调整 $ \gamma $ 的有效性)
论文进一步证明调整跳数聚合参数 $ \gamma $ 是一个有效的方法。命题指出,最优的 $ \gamma $ 依赖于图的度和同质性(即 $ \gamma_{T}^{*} = d_{T}(2h_{T} - 1) $ ),当图从源图变为目标图时,最优的 $ \gamma $ 也会改变。因此在测试时把 $ \gamma $ 调整到目标图的最优值就可以显著缓解表示退化,提升模型准确率。
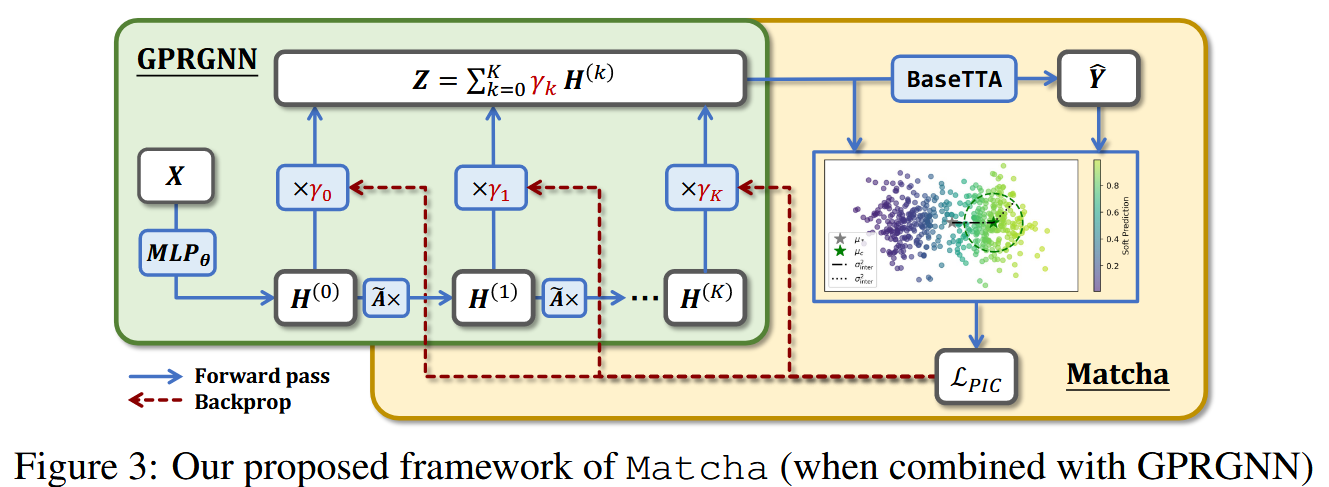
Proposed Framework
基于以上洞察,论文设计了 Matcha 框架,旨在解决两个挑战:1. 在没有标签的情况下,如何更新跳数聚合参数以应对结构偏移? 2. 如何确保算法与现有的 TTA 算法兼容,以同时解决结构和属性偏移?
Prediction-Informed Clustering Loss
传统的 TTA 方法主要采用熵(entropy)作为代理损失函数,但论文发现熵最小化在提升表示质量方面效果有限,因为它对 logits 的尺度敏感,容易导致平凡解。
为了解决这个问题,论文提出了一种新颖的预测感知聚类损失 (Prediction-Informed Clustering, PIC) 损失,其核心思想是:一个好的节点表示应该使得同类节点在特征空间中紧密聚集,而不同类节点则相互远离。
其计算过程如下:
- 计算质心:利用模型当前的软预测结果 $ \hat{Y} $ 作为“伪类别”信息,计算每个伪类别 $ c $ 的质心 $ \mu_c $ 和所有节点的总质心 $ \mu_* $。$$ \mu_{c} = \frac{\sum_{i=1}^{N}\hat{Y}_{i,c}z_{i}}{\sum_{i=1}^{N}\hat{Y}_{i,c}}, \quad \mu_{*} = \frac{1}{N}\sum_{i=1}^{N}z_{i} $$
- 计算方差:计算类内方差 $ \sigma_{intra}^2 $(希望它小)和类间方差 $ \sigma_{inter}^2 $(希望它大)。$$ \sigma_{intra}^{2} = \sum_{i=1}^{N}\sum_{c=1}^{C}\hat{Y}_{i,c}||z_{i}-\mu_{c}||_{2}^{2} $$ $$ \sigma_{inter}^{2} = \sum_{c=1}^{C}(\sum_{i=1}^{N}\hat{Y}_{i,c})||\mu_{c}-\mu_{*}||_{2}^{2} $$
- PIC 损失函数:最终的 PIC 损失被定义为类内方差占总方差的比例。$$ \mathcal{L}_{PIC} = \frac{\sigma_{intra}^{2}}{\sigma_{intra}^{2} + \sigma_{inter}^{2}} $$ 通过最小化这个损失,模型会调整 $ \gamma $ 来优化节点表示 $ Z $,使得类内尽可能紧凑,类间尽可能分离。这种比率形式对表示的尺度不敏感,可以有效避免平凡解。
Integration of Generic TTA Methods
Matcha 框架可以和任何现有的 TTA 方法(论文中称为 BaseTTA)无缝集成。
应用通用 TTA:使用
BaseTTA(如 Tent, T3A)对当前模型进行调整,得到一个初步的软预测 $ \hat{Y} $ 。这一步主要处理属性偏移。更新跳数聚合参数:将 $ \hat{Y} $ 作为伪标签,计算 $ \mathcal{L}_{PIC} $ 损失,并根据该损失的梯度只更新跳数聚合参数 $ \gamma $ 。这一步专门应对结构偏移,以恢复表示质量。
这个过程形成了一种协同效应:通过调整 $ \gamma $ 得到的更好表示,为 BaseTTA 提供了更高质量的输入,使其能做出更准的预测;而更准的预测又为 $ \mathcal{L}_{PIC} $ 提供了更可靠的伪标签,从而更好地指导 $ \gamma $ 的更新。
Experiments
论文在合成数据集(CSBM)和多个真实世界数据集(如 Syn-Cora, Syn-Products 等)上进行了广泛的实验,以验证 Matcha 的有效性。
Matcha Handles Various Structure Shifts
主要结果:
- 与不进行自适应的模型(ERM)相比,单独使用 Matcha(ERM+Matcha)可以显著提升模型性能,在真实世界数据集上最高提升 31.95%。
- 与其他基线方法相比,Matcha 在大多数情况下取得了最佳性能,最高超出 40.61%。
- Matcha 与基线 TTA 方法结合时,能进一步提升它们的性能,最高可达 22.72%(合成数据)和 39.31%(真实数据)。这些结果有力地证明了 Matcha 的有效性。
Matcha Restores The Representation Quality
除了性能提升,论文还通过 t-SNE 可视化方法,验证了 Matcha 是否成功恢复了节点表示的质量。
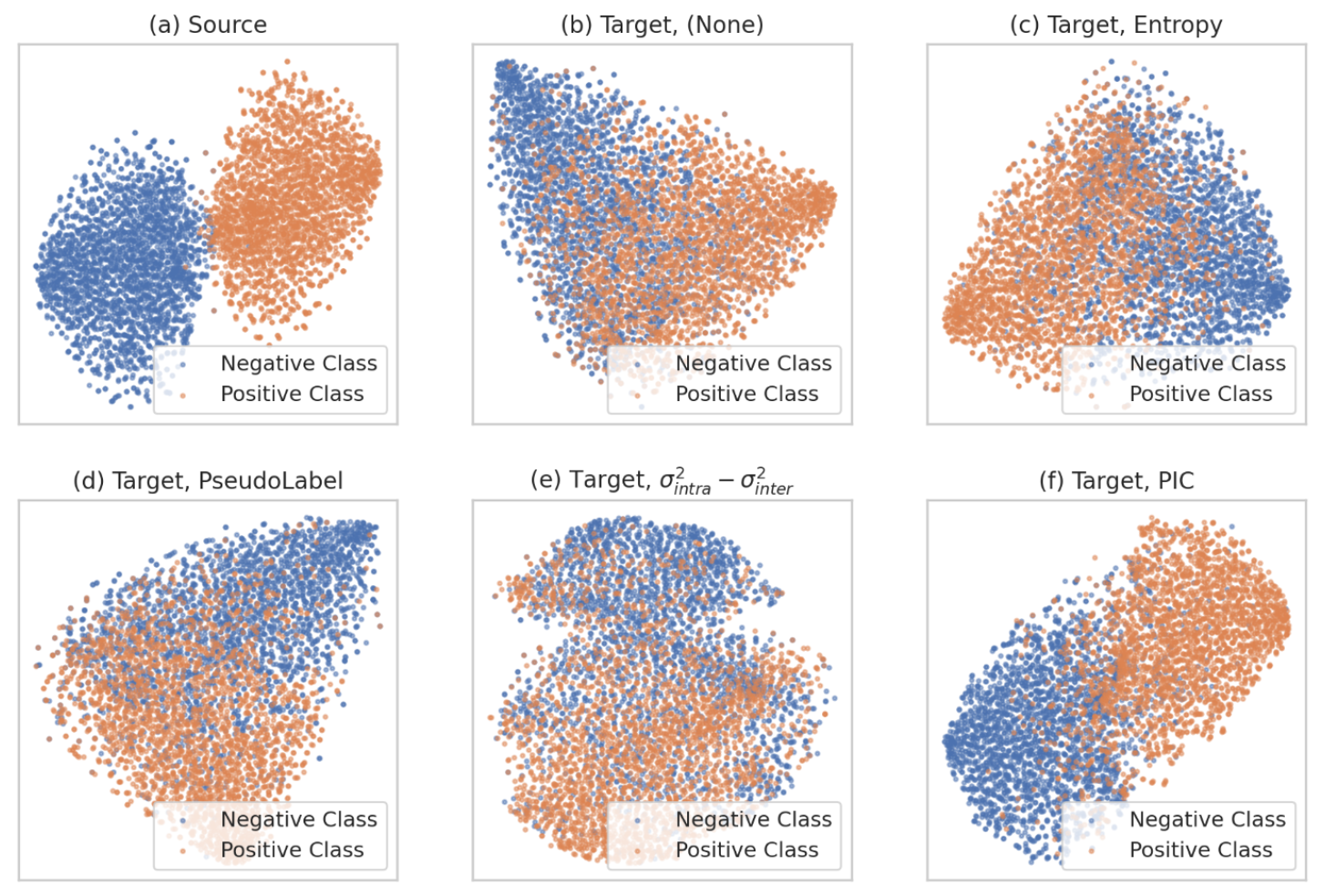
在结构偏移下(b),原始模型的节点表示变得混乱不堪。在使用其他损失函数(c, d, e)后,表示质量虽有改善但仍不理想。而使用 Matcha 的 PIC 损失后(f),节点表示重新形成了非常清晰的聚类结构,证明其成功恢复了表示质量。
Conclusion
本文的贡献可以总结为:
- 理论分析:首次从理论上揭示了属性偏移和结构偏移对 GNN 有着截然不同的影响模式,解释了为何通用 TTA 方法在结构偏移下会失效。
- 提出框架:提出了一个即插即用的 TTA 框架 Matcha,通过一种新颖的预测感知聚类损失(PIC Loss) 来指导跳数聚合参数的自适应调整,从而恢复因结构偏移而退化的节点表示质量。
- 实验验证:在多种数据集和场景下的广泛实验,一致且显著地证明了 Matcha 框架的有效性、高效性和通用性。