SSA | diefish's blog

Introduction

TTA 在回归任务上的局限：为分类任务设计，一般基于熵最小化和特征对齐；熵最小化不适用，回归模型产生单一值，不产生概率分布；简单特征对齐对回归模型效果不佳，可能反而会稀释需要学习的特征

Problem Setting

考虑一个回归模型 $ f_\theta: \mathcal{X} \to \mathbb{R} $，可以进一步分解为特征提取器 $ g_\phi: \mathcal{X} \to \mathbb{R}^D $（从输入 $ \mathcal{X} $ 提取 $ D $ 维特征 $ z $）和线性回归器 $ h_\psi(z) = w^T z + b $（或者 $ h_{\psi}(z)=Wz+b $）

$ f_\theta $ 首先在一个有标签的源数据集 $ S = \{(x_i, y_i)\}_{i=1}^{N_s} $ 上进行预训练，数据从源域分布 $ p_s $ 中采样

目标是使用一个无标签的目标数据集 $ T = \{x_j\}_{j=1}^{N_t} $ 来适应预训练好的模型 $ f_\theta $ 到目标域

我们假设存在 covariate shift ，这意味着：

输入数据的分布在源域和目标域之间是不同的：$ p_s(x) \neq p_t(x) $
但给定输入后，输出的条件分布是相同的：$ p_s(y|x) = p_t(y|x) $

Test-time Adaptation for Regression

Basic Idea: Feature Alignment

朴素实现：

计算源域特征统计量：在源域训练后，计算源域特征的均值 $ \mu^s $ 和元素级方差 $ \sigma^{s2} $ $$ \mu^s = \frac{1}{N_s} \sum_{i=1}^{N_s} z_i^s, \quad \sigma^{s2} = \frac{1}{N_s} \sum_{i=1}^{N_s} (z_i^s - \mu^s) \odot (z_i^s - \mu^s) \quad \text{(1)} $$ 其中 $ z_i^s = g_\phi(x_i) $ 是源特征，$ N_s $ 是源数据样本数，$ \odot $ 表示元素级乘积
目标域特征统计量：在目标域，对每个迷你批次（mini-batch）$ B = \{x_j\}_{j=1}^{N_B} $，计算其特征均值 $ \hat{\mu}^t $ 和方差 $ \hat{\sigma}^{t2} $，计算方式与公式 (1) 类似
对齐损失函数：使用 KL 散度来衡量两个对角高斯分布 $ N(\mu^s, \sigma^{s2}) $ 和 $ N(\hat{\mu}^t, \hat{\sigma}^{t2}) $ 之间的差异，并最小化该差异。 $$ L_{TTA} (\phi) = \frac{1}{2} \sum_{d=1}^D \left\{ D_{KL} (N(\mu^s_d, \sigma^s_{d}{}^2)||N(\hat{\mu}^t_d, \hat{\sigma}^t_{d}{}^2)) + D_{KL} (N(\hat{\mu}^t_d, \hat{\sigma}^t_{d}{}^2)||N(\mu^s_d, \sigma^s_{d}{}^2)) \right\} \quad \text{(2)} $$ 这里的 $ d $ 表示向量的第 $ d $ 个元素。之所以使用双向的 KL 散度，是为了经验上获得更好的结果
一维高斯 KL 散度公式： $$ D_{KL} (N(\mu_1, \sigma_1^2)||N(\mu_2, \sigma_2^2)) = \dfrac{\left[ \log(\sigma_2^2/\sigma_1^2) + \dfrac{(\mu_1 - \mu_2)^2 + \sigma_1^2}{\sigma_2^2} - 1 \right]}{2} \quad \text{(3)} $$
朴素对齐的问题：
- 回归模型特征倾向于分布在一个小型的子空间中，许多特征维度方差为零或接近零
- 公式 (3) 中涉及到方差在分母上，使得这种朴素对齐在面对零方差维度时变得不稳定
- 对所有维度“一视同仁”地对齐不适用于回归任务的特性，因为许多维度对最终输出影响很小

Significant-subspace Alignment

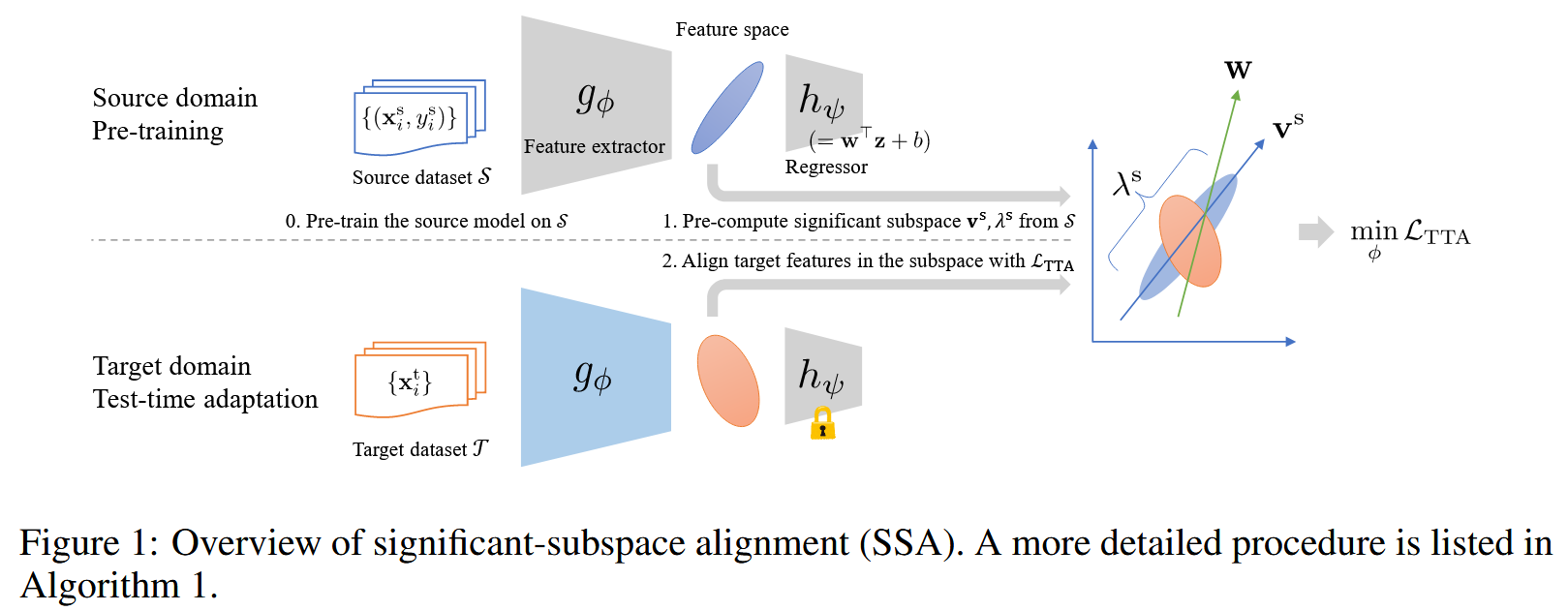
SSA 的三个步骤：

子空间检测 (Subspace detection)：
- 在源数据集 $ S $ 上进行训练后，检测源特征分布所在的子空间。不计算每个维度的方差，而是计算协方差矩阵： $$ \Sigma^s = \frac{1}{N_s} \sum_{i=1}^{N_s} (z_i^s - \mu^s) (z_i^s - \mu^s)^T \quad \text{(4)} $$ 其中 $ \mu^s $ 是源特征的均值向量（同理 (1)）
- 基于 PCA 的思想，通过对 $ \Sigma^s $ 进行特征分解，得到特征向量 $ v_d^s $ 和对应的特征值 $ \lambda_d^s $
- 选取前 K 个最大的特征值 $ \lambda_1^s, \dots, \lambda_K^s $ 及其对应的源基向量 $ v_1^s, \dots, v_K^s $ 来定义源子空间，这些基向量张成的子空间代表了源特征数据最有代表性和最重要的变化方向
维度加权 (Dimension weighting)：
- 考虑到回归模型 $ h_\psi(z)=w^T z + b $，子空间维度 $ v_d^s $ 对最终输出的影响由 $ w^T v_d^s $ 决定（即特征向量与回归器权重向量的点积）
- 为了优先对齐那些对输出影响更大的子空间维度，为每个子空间维度 $ d $ 定义权重 $ a_d $： $$ a_d = 1 + |w^T v_d^s| \quad \text{(5)} $$ 这个权重 $ a_d $ 会在对应的子空间基方向对输出有较大影响时值更大（最小为 1）。
特征对齐 (Feature alignment)：
- 这一步在目标域进行。对于目标域的迷你批次 $ B $，首先将目标特征 $ z^t = g_\phi(x^t) $ 投影到源子空间。 $$ \tilde{z}^t = V_s^T (z^t - \mu^s) \quad \text{(6)} $$ 其中 $ V_s = [v_1^s, \dots, v_K^s] \in \mathbb{R}^{D \times K} $ 是由前 K 个源基向量构成的矩阵，$ \tilde{z}^t \in \mathbb{R}^K $ 是投影后的目标特征。
- 然后，计算投影后目标特征的迷你批次均值 $ \tilde{\mu}^t $ 和方差 $ \tilde{\sigma}^{t2} $ （同理公式 (1) ）
- 最后，使用结合子空间检测和维度加权的新损失函数来最小化目标特征分布与源特征分布在子空间中的差异。源域投影后的均值是 0，方差是其特征值 $ \Lambda^s = [\lambda_1^s, \dots, \lambda_K^s] $。 $$ \begin{align}L_{TTA}(\phi) = & \frac{1}{2} \sum_{d=1}^K a_d \left\{ D_{KL} (N(0, \lambda^s_d)||N(\tilde{\mu}^t_d, \tilde{\sigma}^t_{d}{}^2)) + D_{KL} (N(\tilde{\mu}^t_d, \tilde{\sigma}^t_{d}{}^2)||N(0, \lambda^s_d)) \right\} \\ = & \sum_{d=1}^K a_d \left\{ \frac{(\tilde{\mu}^t_d)^2 + \lambda^s_d}{2\tilde{\sigma}^t_{d}{}^2} + \frac{(\tilde{\mu}^t_d)^2 + \tilde{\sigma}^t_{d}{}^2}{2\lambda^s_d} - 1 \right\} \quad \text{(7)} \end{align} $$ 其中 $ a_d $ 是维度权重，$ \lambda_d^s $ 是源域子空间的第 $ d $ 个特征值，$ \tilde{\mu}_d^t $ 和 $ \tilde{\sigma}_{d}{}^2 $ 是投影后的目标特征在第 $ d $ 个维度上的均值和方差

伪代码：

输入：预训练好的源模型 $ f_\theta $、源基向量 $ V_s $、源均值 $ \mu^s $、源方差 $ \Lambda^s $、目标数据集 $ T $
输出：适应后的模型 $ f_\phi^t $
步骤：
- 计算源子空间中每个维度的权重 $ a_d $
- 对于目标数据集 $ T $ 中的每个 mini batch $ \{x\}_i^B $：
  - 提取目标特征 $ z = g_\phi(x) $。
  - 将目标特征投影到源子空间 $ \tilde{z} $
  - 计算投影后目标特征的均值 $ \tilde{\mu}^t $ 和方差 $ \tilde{\sigma}^{t2} $
  - 更新特征提取器 $ g_\phi $ 以最小化损失函数 $ L_{TTA}(\phi) $
- 重复直到收敛。

对角高斯分布的合理性

为什么假设特征分布为对角高斯分布是合理的：

中心极限定理：当特征被投影到子空间后，如果原始特征维度 $ D $ 足够大，根据中心极限定理，投影后的特征分布会倾向于高斯分布。
PCA 的去相关性：由于子空间检测使用了 PCA，投影到主成分上的特征是去相关的，这意味着不同维度之间是独立的，这使得对角高斯分布的假设（即各维度独立）变得合理。

Appendix

A. LIMITATION：SSA 假设是协变量偏移，即 $ p(y|x) $ 不变，未来工作将考虑 $ p(y|x) $ 变化的情况
B. EVALUATION METRIC：R²接近 1 表示模型拟合效果好 $$ R^2 = 1 - \frac{\sum_{i=1}^N (y_i - \hat{y}_i)^2}{\sum_{i=1}^N (y_i - \bar{y})^2} \quad \text{(10)} $$ 其中 $ \hat{y}_i $ 是预测值，$ y_i $ 是真实值，$ \bar{y} $ 是真实值的平均值。
D. ADDITIONAL EXPERIMENTAL RESULTS：
- D.1 特征对齐的度量：比较了 KL 散度、2WD 和 L1 范数作为特征对齐损失的效果，结果显示 KL 散度结合子空间检测（SSA）表现最佳。
  - 公式 (11)：2-Wasserstein Distance for Gaussians $$ W_2^2 (N(\mu_1, \sigma_1^2), N(\mu_2, \sigma_2^2)) = (\mu_1 - \mu_2)^2 + (\sigma_1 - \sigma_2)^2 $$
  - 公式 (12)：L1 Norm of Statistics $$ L_1 (N(\mu_1, \sigma_1^2), N(\mu_2, \sigma_2^2)) = |\mu_1 - \mu_2| + |\sigma_1 - \sigma_2| $$
  - 公式 (13)：SSA Loss with 2WD $$ L_{TTA-2WD} = \sum_{d=1}^K a_d \left\{ (\tilde{\mu}^t_d)^2 + (\tilde{\sigma}^t_d - \sqrt{\lambda^s_d})^2 \right\} $$
  - 公式 (14)：SSA Loss with L1 Norm $$ L_{TTA-L1} = \sum_{d=1}^K a_d \left\{ |\tilde{\mu}^t_d| + |\tilde{\sigma}^t_d - \sqrt{\lambda^s_d}| \right\} $$
- D.2 特征可视化：通过 PCA 和 UMAP 等降维技术可视化了源域和目标域特征分布（图 4-5），直观地展示了 SSA 如何成功地将目标特征分布拉近源域。
- D.3 原始特征维度对子空间的影响：分析了原始特征维度对子空间的重要性。
  - 公式 (15)：Gradient Norm $ s_d $ $$ s_d = ||\frac{\partial \tilde{z}}{\partial z_d}||_2 = ||(V_s^T)_d||_2 = ||[v_{1,d}^s, \dots, v_{K,d}^s]||_2, $$ 其中 $ (V_s^T)_d $ 是 $ V_s^T $ 的第 $ d $ 行。
  - 发现：回归模型的特征子空间确实受许多原始特征维度影响很小（图 6），这进一步确认了子空间检测的必要性。
- D.4 附加消融实验：进一步证实了子空间检测对于 SSA 性能的重要性（表 13-14）。
- D.5 Vision Transformer 实验：在 Vision Transformer 上验证了 SSA 的有效性（表 15-16），表明该方法对不同模型架构也适用。
- D.6 多任务回归模型：将 SSA 应用于多任务回归，模型同时输出多个预测值（如头部姿态的俯仰、偏航、滚转角度），结果表明 SSA 同样有效（表 17）。
- D.7 与分类 TTA 结合：探索了 SSA 与分类 TTA 结合的可能性（表 18-20）。
- D.8 超参数敏感性：分析了学习率和批次大小等超参数对 SSA 性能的影响（表 21-26），发现 SSA 在典型参数范围内表现稳定。
- D.9 额外结果：提供了 MAE 等其他指标的性能数据（表 27-28）。
- D.10 在线设置：SSA 在分批在线（batched online）设置下也表现出色（表 29-31）。

Introduction#

Problem Setting#

Test-time Adaptation for Regression#

Basic Idea: Feature Alignment#

Significant-subspace Alignment#

对角高斯分布的合理性#

Appendix#