Method
Problem Set
EEG 数据 $ \{ X_{s,l}^{i},y_{s,l}^{i} \}_{i=1}^{n_{s,l}} $ ,进行无监督在线 K 分类
Source Model Training
对源数据做 Euclidean alignment (EA) 数据对齐,减少不同个体 EEG 信号差异
EA 计算每个个体所有 EEG 试次协方差矩阵的算术平均值 $$ R_{s,l} = \dfrac{1}{n}\sum_{i=1}^{n} X_{i}(X_{i})^{T} \implies \bar{X}_{i} = R_{s,l}^{-1/2}X_{i} $$ 之后再整合经过对齐的受试者数据,形成“源域”
在整合后的数据上独立训练 $ M $ 个模型
Incremental EA on Target Data
对新数据增量式更新协方差矩阵,再用新的矩阵更新所有测试数据
Target Label Prediction
用训练好的 $ M $ 模型初始化用于适应目标域的 $ M $ 个 TTA 模型 $ f_{m} $
新的 $ X_{a} $ 经过 IEA 被变换为 $ X_{a}' $ 后被输入到每个模型 $ f_{m} $ 中进行分类,输出概率向量 $ f_{m}(X_{a}') $
之后结合这 $ M $ 个概率向量来获得最终的预测标签 $ \hat{y}_{a} $
- $ a\leq M $ 数据量较少:直接对所有模型的预测向量平均
- $ a>M $ 数据量较多:使用谱元学习器对各个模型进行加权平均,根据历史表现(预测的协方差矩阵)分配不同的权重
Target Model Update
在数据量足够以后($ a>B $)使用一个滑动批次的数据更新模型,在此之前模型不变
组合损失函数: $$ L_{M} = L_{CEM}(f_{m};\{ X'_{i} \}_{i=a-B+1}^{a}) + L_{MDR}(f_{m};\{ X'_{i} \}_{i=a-B+1}^{a}) $$ 有两个部分
1) Conditional Entropy Minimization 条件熵最小化
- 使分类边界更加清晰
- 通过最小化每个预测的条件熵(使用温度缩放因子 $ T $ 进行校准),使模型倾向于输出接近 0 或 1 的概率
2) Adaptive Marginal Distribution Regularization 自适应边缘分布正则化
- 防止出现所有数据都在单类别和对错误结果过于自信的不良结果
- 计算当前批次每个类别的平均预测概率 $ p_{k} $
- 通过设置阈值得到伪标签,估计目标域的类别评论 $ z_{k} $
- 校准平均预测概率 $ q'_{k} $ $$ q_{k} = \dfrac{p_{k}}{c+z_{k}},\quad q'_{k} = \dfrac{q_{k}}{\sum q} $$
- $ L_{MDR} = \sum_{k=1}^{K}q'_{k}\log q'_{k} $ (采用负熵的形式)
Complete T-TIME Algorithm
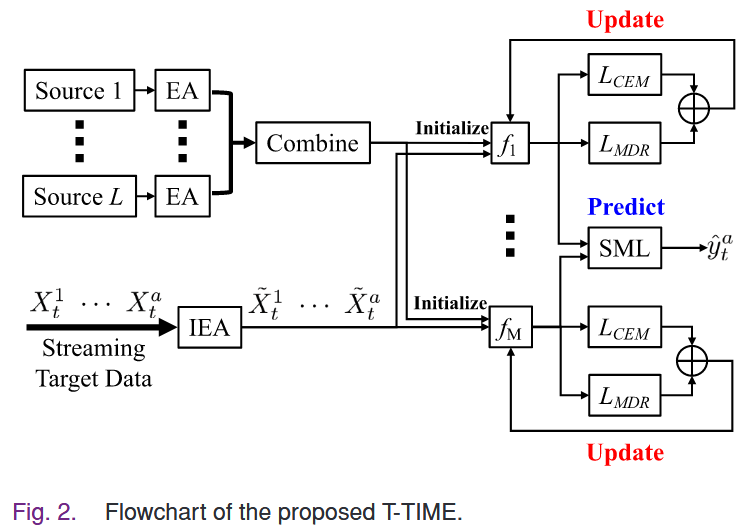
先预测,后台并行地更新模型
Experiment
使用三个运动想象数据集
每次把一个受试者的数据作为目标域,其余作为源域
Classification Accuracies on Balanced Classes
- 过于复杂的算法由于数据不足,性能反而下降
- 基于熵的方法普遍表现良好,MCC 在离线迁移学习中表现最好
- T-TIME 在所有在线迁移学习算法中表现最佳,并且其性能与表现最佳的离线迁移学习方法相当
Classification Performance Under Class-Imbalance
使用随机移除数据来创建不平衡数据集
- 传统方法表现较弱
- T-TIME 表现突出